אין
קוואנטום פיזיקס איז דא די געדאנק פון
ספּין. בקיצור נמרץ מאד מאד און אָווערסימפּליפייד איז דאס די ענגולער מאָמענטום פונעם פּארטיקל. והגם די פּארטיקל ״דרייט״ זיך דאך נישט בעצם באמת איז דאס אבער די כח וואס דאס האט
אינטרינסיקלי אין זיך ביסודה פון אזא סארט מאָמענטום.
ועפי״ז ווערן די קוואנטום עלעמענטערי פּארטיקלס צוטיילט אין צו צוויי סוגים:
פערמיִאַנס, וואס זענען די פּארטיקלס וואס שטעלן צאם החומר כולה [קוואַרקס, עלעקטראנס/לעפּטאַנס אא״וו], און
בּאָסאַנס, וואס זענען די פּארטיקלס וואס פירן די
פונדאמענטאלע פאָרסעס [עלעקטראָמאגנעטיזם, שטארקע נוקלעארע כח וכו׳; פאָטאַן, גלוּאַן וכו׳]. די
פערמיִאַנס קענען נאר האבן א ½
ספּין, מיינענדיג אז זייער
ספּין קען נאר זיין א מאָלטיפּל פון ½ [מיינענדיג ½, ½1, ½2, אא״וו; עס דארף האבן א ½ אין זיך] פונעם רעדוצירטער
פּלאנק קאַנסטענט [ħ]
(די קאנסטענט בכלליות רעכענט דאך די ענערגיע פּער סייקעל/פריִקווענסיִ פון א וועיוו, די רעדוצירטער קאַנסטענט איז ווען מ׳עקספּרעסט עס אין טערמינען פון ״ענגולער״ פריִקווענסיִ), און
בּאָסאַנס קענען נאר האבן א גאנצע-נומער [אינטעדזשער] מאָלטיפּל דערפון. דאס איז די
ספּין-סטאטיסטיקס טעארעם.
ס׳איז טאקע דא די היפּאטעזיע פון סוּפּערסימעטרי וואס לויטעט אז יעדעס פערמיִאַן האט א גענויע בּאָסאַן וואס איז די זעלבע ווי די פערמיִאַן בכל פרטיה אחוץ איר ספּין וואס איז אזוי ווי א בּאָסאַן, און דאס זעלבע פארקערט אז יעדעס בּאָסאַן האט א גענויע פערמיִאַן וואס איז די זעלבע ווי די בּאָסאַן בכל פרטיה אחוץ איר ספּין וואס איז אזוי ווי א פערמיִאַן. מען האט אבער (נאך) נישט געטראפן די סארט פּאַרטיקלס.עס קומט אויס אז ביי
פערמיִאַנס איז דא די
פּאָליִ עקסקלוּזשען פּרינציפּ. דאס לויטעט אז עס קענען נישט זיין אין איין סיסטעם צוויי זעלבע סארט
פערמיִאַנס וואס זאלן האבן אלע זייערע (פיר) קוואנטום נומערן די זעלבע. עפי״ז קומט אויס אז ביי עלעקטראנס, וואס זענען
פערמיִאַנס מיט ½
ספּין, וועלן נישט קענען פארנעמען די זעלבע ״מקום״/סטעיט אין אַן אָרבּיטעל [כעין די ״רינגען״ פון די עלעקטראַנס אין אן אטאם וואס נעמען ארום די נוּקלעאס פונעם אטאם וואו די פּראָטאַנס און ניוּטראַנס געפינען זיך]. משא״כ ביי
בּאָסאַנס וואס האבן א גאנצע-נומער
ספּין איז דאס נישט א פראבלעם. דאס איז מכח דעם אז די טאטאלע וועיוו-פאָנקשען (פון אפאר פּארטיקלס) פון
פערמיִאַנס מוז זיין אנטיסימעטריק, וואס דאדורך איז דאס מאטעמאטיש מוכרח, און די פון
בּאָסאַנס מוז זיין סימעטריק, וממילא איז דאס נישט מאטעמאטיש מוכרח ולכן וויבאלד אין נאטור וויל אלעס גיין צום נידעריגסטן ענערגיע סטעיט גייען און קענען זיי אלע זיין אינעם זעלבן סטעיט בתוך די נידעריגע ענערגיע לעוועל.
(דאס איז הגם אז אין קוואנטום מעכאניקס קען מען נישט פונאנדערשיידן סיי צווישן צוויי זעלבע פערמיִאַנס און סיי צווישן צוויי זעלבע בּאָסאַנס; זיי זענען אידענטיקאל. מיינענדיג, אז אויב עס טוישן זיך אויף די מקום פון איין עלעקטראַן וכדומה מיט אן אנדערע וועט מען דאס נישט קענען וויסן. עס איז ביסודו אומעגליך דאס צו וויסן און פונאנדערשיידן. ואגב, טוהט די געדאנק פארענטפערן גיבּס׳/מישן פּאראדאקס. דאס האט געוואוזן מאטעמאטיש אז אויב איך האב צוויי קאנטעינערס וואס זענען גענוי די זעלבע און זענען ביי טערמאָדינאמיק עקוויליבּריִאוּם [וואו עס איז נישטא קיין, עכ״פ מעקראָסקאַפּיק ונראה לעינים, אויסטויש פון ענערגיע וכו׳] און דערנאך נעם איך אוועק די וואנט צווישן זיי וועט די ענטראָפּי ארויפגיין דורכ׳ן דאס אויסמישן יעצט פון די פּארטיקלס וכו׳. אבער דערנאך ווען איך לייג צוריק די וואנט, מיט׳ן בלויז דאס טוהן, גייט די ענטראָפּי אראפגיין! אין קעגנזאץ צום צווייטן געזעץ. אבער אויב זענען זיי מעיקרא איידענטיקל כנ״ל האט דאך דאס׳ן אוועקנעמען די וואנט גארנישט צוגעגעבן צום ענטראָפּי מעיקרא אפילו עפ״י מאטעמאטיקס. און טאמער זענען זיי צוויי יא געווען מעיקרא אנדערש דאן טוהט דאס׳ן צוריקשטעלן די וואנט נישט נידערן די ענטראָפּי.)בשעת
פערמיִאַנס וועלן נאכגיין
פערמיִ-דיראק סטאטיסטיקס צו קובע זיין די עוורידזש פון די ענערגיע וכו׳ פון די פּאַרטיקלס (וואס לכן ווערן די פּאַרטיקלס גערופן ״
פערמיִאַנס״) ווען זיי זענען אין טערמאָדינאמיק עקוויליבּריִאוּם, וועלן
בּאָסאַנס נאכגיין
בּוֺיס-איינשטיין סטאטיסטיקס (וואס לכן ווערן די פּאַרטיקלס גערופן ״
בּאָסאַנס״) ווען זיי זענען אין טערמאָדינאמיק עקוויליבּריִאוּם. (דאס וועט צב״ש מעסטן די פּראבּעבּיליטי אז א פּאַרטיקל זאל אריבערגיין די
פערמי לעוועל פון די
וועילענס בּענד צו די
קאַנדאָקטינג בּענד.) ביידע סטאַטיסטיקס זענען מיוסד אויף די
מעקסוועל-בּאָלטצמאן סטאטיסטיקס וואס מעסט די עוורידזש דיסטריבּיוּשאן
(כעין ענין זה) פון די ענערגיע פון פּאַרטיקלס ביי טערמאַל עקוויליבּריִאוּם ביי א געוויסע טעמפּעראטור ביי קלאסישע פיזיקס.
די קוואנטום סטאטיסטיקס נעמען איבער, ביי די רעספּעקטיווע סארט פּארטיקלס [
בּאָסאַנס אדער
פערמיִאַנס], ווען מ׳קען טאקע נישט פונאנדערשיידן צווישן איין פּאַרטיקל און אן אנדערע פון די זעלבע סארט כנ״ל, און ווען די דענסיטי פון די פּאַרטיקלס [די צאל פון די פּאַרטיקלס רעלאטיוו צו די וואַליוּם אין וואו זיי געפינען זיך] איז מער אדער דאס זעלבע גענוי ווי
קוואנטום קאַנסענטרעישאן. די
קוואנטום קאַנסענטרעישאן באדייט אז בעצם איז דאך אלע חומר אליינס, זייענדיג למעשה צאמגעשטעלט פון קוואנטום פּאַרטיקלס, אליינס א וועיוו; די
דע בּראָגלי וועיוולענגט. ווען מ׳וויל דאס מעסטן ביי א געוויסע טעמפּעראטור איז די עוורידזש
דע בּראָגלי וועיוולענגט דערפון ביי יענע געוויסע טעמפּעראטור די
טערמאל דע בּראָגלי וועיוולענגט דערפון. מ׳קען באטראכטן אז די עוורידזש מרחק צווישן איין פּאַרטיקל און א צווייטן צו זיין די קיוּבּיק-רוּט פון די וואַליוּם דערפון דיוויידעד ביי די צאל פּאַרטיקלס. אויב איז די וועיוולענגט היבש קלענער ווי דעם איז עס בעצם א נארמאלע גאז נאכגייענדיג
מעקסוועל-בּאָלטצמאן סטאטיסטיקס. אויב אבער איז דאס די זעלבע אדער גאר מער דאן נעמען איבער די קוואנטום סטאטיסטיקס. והיינו, אויב איז די מאסע פון די סארט פּאַרטיקלס אינעם חשבון טיימס די
בּאָלטצמאן קאַנסטענט טיימס די טעמפּעראטור [געמאסטן אין קעלווינס] און דאס אלעס דיוויידעד ביי צוויי מאל π טיימס די סקווער פונעם רעדוצירטן
פּלאנק קאַנסטענט, דערנאך קיוּבּ איך דאס אלעס און דערנאך נעם איך די סקווער-רוּט, און דאס אלעס איז ווייניגער צו דאס זעלבע ווי די דענסיטי דאן איז די ווייטקייט צווישן די פּאַרטיקלס אזוי אז זייערע
דע בּראָגלי וועיוולענגט טוהן ממש אָווערלעפּן איינע אויף די אנדערע.
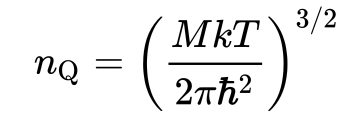
- 8F9CD77D-6312-4F55-8338-8A18ABDBBE1C.jpeg (15.91 KiB) געזען געווארן 4523 מאל
ועפי״ז און אז זעלבע
בּאָסאַנס קענען פארנעמען די זעלבע סטעיט ווי אנדערע
בּאָסאַנס איז ביי גאר קליינע טעמפּעראטורס (א טריליאנסטל העכער
אַבּסאַלוט זערא) וועלן אן אומצאליגע צאל פון זיי ״קאָנדענסן״ אין צו א גאר קליינע ענערגיע סטעיט אזוי ווי די ארומיגע טערמאַל ענערגיע וואס איז קליין. דאס קען אויך געשעהן מיט געוויסע אטאמען ווען זיי ווערן אזוי שטארק אפגעקילט [אויב עס איז א קאַמפּאַזיט/צאמגעשטעלטע פּאַרטיקל וואס האט אן איִווען צאל
פערמיִאַנס - היינו, עס איז עלעקטריקעלי נייטראל, האבענדיג די זעלבע צאל פּראָטאַנס ווי עלעקטראַנס, און עס האט אַן איִווען צאל פון ניוּטראַנס]. דאס איז די באקאנטע
בּוֺיס-איינשטיין קאַנדענסעיט וואו, זייענדיג אז עס איז א סאך מייקראסקאפּיק פּאַרטיקלס ביינאזאם וואס פירן זיך אויף מיט די קוואנטום ״הלכות״, מ׳קען זעהן אויף א מעקראָסקאַפּיק לעוועל קוואנטום עפעקטס. עס ווערט ווי א גאנץ נייע פיפטע פעיס פון מעטער [ווי די אנדערע פיר זענען, ווי באקאנט, סאַליד, ליקוויד, גאז, און פּלאַסמאַ]. די טעמפּעראַטור וואס מ׳דארף צוקומען דאס צו שאפן איז ווען איך נעם די דענסיטי פון די פּאַרטיקלס, והיינו וויפיל פון די פּאַרטיקלס איז דא פּער די וואליום/מקום וואו איך רעכען [וואו ״צושטופט״ זיי זענען כנ״ל] און איך דיווייד דאס ביי די
ריעמאַן זעטאַ פאָנקשען פון 1 און אהאלב (וואס קומט אויס צו בערך 2.6124). דערנאך סקווער איך די נומער וואס איך באקום דערפון און דערנאך נעם איך די קיוּבּיק-רוּט פון די נומער וואס איך באקום יעצט. דערנאך מאָלטיפּליי איך די סקווער פון די רעדוצירטער
פּלאנק קאַנסטענט ביי 2 מאל π און איך דיווייד דאס ביי די
בּאָלטצמאן קאַנסטענט טיימס די מאסע פון די סארט
בּאָסאַן וואס פון זיי וויל איך מאכן די קאַנדענסעיט. דערנאך מאָלטיפּליי איך די נומער וואס איך באקום מיט די נומער וואס איך האב באקומען פונעם פריערדיגן קיוּבּיק-רוּט:
עס האט געדויערט אן ערך פון 70 יאר פון ווען מ׳האט דאס טעארעטיש פּאָזיטירט ביז מען האט דאס באשיינפערליך געזעהן אין עקספּערימענטס.
{התנצלות: דאס איז אלעס כמובן נישט מיט אן עיון און גראָסלי אָווערסימפּליפייד. ואתכם הסליחה.}
מ׳האט גענוצט דעם געדאנק פון בּוֺיס-איינשטיין קאַנדענסעיט אין אן עקשאָן פילם אויף נעטפליקס ספּעקטראל. דא צונעמט עס דר. טיִלאָ סטאָפערלע, א פיזיקער וואס שטודירט בּוֺיס-איינשטיין קאַנדענסעיטס.