אין דעם געביט איז דא די געדאנק פון
בּערנוֺיליִ נומערן. מאטעמאטיקער האבן אלס געזוכט ווי אזוי צו האבן א גענעראלע פארמולע אויף צו לעזן (פיניט) סיריִס וואס האבן סאָקסעסיוו קאנסעקיוטיוו נומערן איינס נאכ׳ן אנדערן און אלע געהעכערט צום זעלבן עקספּאנענט. דער מאטעמאטיקער יעקב בּערנאָלי (ווי אויך דער יאפאנעזער מאטעמאטיקער סעקיִ טאַקאַקאַזוּ אין די זעלבע תקופה) איז אויפגעקומען מיט א סוג פון נומערן, וואס העלפן דאס לעזן, וואס ווערן גערופן
בּערנאָלי נומערן. די נומערן קען מען באקומען דורך די
זעטאַ פאָנקשען. והיינו, אז איך וויל באקומען א [פאזיטיווע]
בּערנאָלי נומער פון א געוויסע פלאץ [כדוגמא די ״דריטע״
בּערנאָלי נומער], דעמאלטס נעם איך 1 און איך נעם אוועק די פלאץ נומער דערפון (וואס וועט דאל בדרך כלל זיין נעגאטיוו) און איך לייג דרס אריין אינעם
זעטאַ פאָנקשען, און וואס עס געבט מיר ארויס מאָלטיפּליי איך ביי נעגאטיוו פון דעם פלאץ נומער. די נומער וואס איך באקום איז די
בּערנאָלי נומער פון יענעם פלאץ.
אן אנדערן וועג פון באקומען/דזשענערעיטן
בּערנאָלי נומערן איז דורך דעם געדאנק פון א
בּיינוֺימיִעל קאָעפישׁענט.
דא הא׳מיר אביסל מסביר געווען דעם געדאנק פון א
פּאַליִנוֺימיִעל עקוועישאן. א
בּיינוֺימיִעל עקוועישאן איז פשוט א פּאַליִנוֺימיִעל וואס איז נאר צאמגעשטעלט פון צוויי טערמינען [צוויי
מאַנוֺימיִעלס]; יעדעס איינס מיט א געהעריגע נומער [די קאָעפישענט ביי וועלכעס עס איז מאָלטיפּלייד; וואס קען זיין 1, וממילא שרייבט מען נאר ארויס די וועריעבּל], א וועריעבּל [וואס קען זיין געהויבן צו אן עקספּאנענט פון 0, וממילא שרייבט מען עס נישט ארויס], און אן אנדערע (בדרך כלל נאר פאזיטיווע) עקספּאנענט פאר יעדעס איינס [וואס איינע פון זיי קען זיין 1, וממילא שרייבט מען עס נישט ארויס].
אויב האב איך א בּיינוֺימיִעל וואס די גאנצע בּיינוֺימיִעל
צוזאם ווערט געהעכערט צו אן עקספּאנענט, והיינו אז איך בין כופל די
גאנצע בּיינוֺימיִעל אויף זיך אליין אזויפיל מאל ווי די עקספּאנענט זאגט מיר, גייט דאס ווערן עקספּענדעד אין צו א פּאַליִנוֺימיִעל עקוועישאן [מיט אנדערע עקספּאָנענטס פאר יעדעס איינס]. עס קומט אויס אז פאר
יעדעס סארט בּיינוֺימיִעל וואס איך עקספּענד אויף אזא וועג, אויב שטעל איך דאס אויס די רעזאָלטינג פּאַליִנוֺימיִעל וואס קומט ארויס פונעם וועריעבּל וואס האט דעם גרעסטן עקספּאנענט [די דעגריִ] ביז דעם קלענסטן, גייט עס
אלס האבן די זעלבע קאָעפישענטס ביי יענעם מקום, ווענדענדיג זיך אינעם עקספּאנענט צו וועלכעס איך האב געהויבן דעם גאנצן אריגינעלן בּיינוֺימיִעל. דאס ווערט ארויסגעשריבן אזוי:
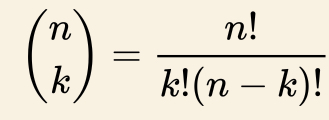
- IMG_8503.jpg (21.21 KiB) געזען געווארן 6212 מאל
דאס מיינט אז די העכערע נומער [n] איז די עקספּאנענט צו וועלכעס איך האב געהויבן דעם גאנצן אריגינעלן בּיינוֺימיִעל, און די אונטערשטע [k] איז די פלאץ אינעם פּאַליִנוֺימיִעל עקספּענשׁאָן דערפון. עס וועט אלס זיין די
פעקטאָריעל פונעם עקספּאָנענט דיוויידעד ביי די פעקטאָריעל פונעם פלאץ-נומער נאך דעם וואס איך האב דאס מאָלטיפּלייד ביי די פעקטאָריעל פונעם חילוק צווישן די צוויי נומערן (דאס איז די
קאַמבּינעישאן פון דעם). מ׳קען גראד זעהן די
בּיינוֺימיִעל קאָעפישענטס פון
פּאַסקאַל׳ס טרייענגעל. יעדעס רוֺי דערין איז כנגד די נומער פון די עקספּאנענט צו וואס כ׳האב געהעכערט דעם אריגינעלן בּיינוֺימיִעל [די העכסטע שורה איז אן עקספּאנענט פון 0] און דערנאך, פון רעכטס צו לינקס, זענען די נומערן, אין א רייע, די קאָעפישענטס פון דעם פּאַליִנוֺימיִעל עקספּענשׁאָן. פון דעם קומט אויס
פּאַסקאַל׳ס רוּל. דאס זאגט אז די בּיינוֺימיִעל קאָעפישענט פון א נומער וועט זיין די סומע פון די נומער וואס איז אויף דעם זעלבן פלאץ ווען די אריגינעלע בּיינוֺימיִעל האט אן עקספּאנענט וואס איז 1 ווייניגער, צוזאמען מיט די נומער וואס איז 1 פלאץ פאר איר ווען די אריגינעלע בּיינוֺימיִעל האט אן עקספּאנענט וואס איז 1 ווייניגער.
מ׳קען באקומען דאדורך די
בּערנוֺיליִ נומערן וואס מען זוכט, והיינו א געוויסע
בּערנוֺיליִ נומער פלאץ, דורך אזא מהלך:
מ׳הייבט אָן פון 0 ביז די מספר
בּערנוֺיליִ נומער וואס מ׳זוכט, און פון 0 דיווייד מען 1 ביי איינס מער ווי די נומער וואו מ׳האלט.
ווען איך האלט ביי א געוויסע נומער דערין אין דעם פראצעס (וואו איך האב אנגעהויבן פון 0) הייב איך אָן אין
דעם גופא פון 0 ביז דעם נומער וואו איך האלט, און ביי יעדעס נומער וואו איך האלט
יעצט וועל איך דאס לייגן אלס אַן עקספּאנענט צו 1-, און דאס מאָלטיפּלייען ביי די בּיינוֺימיִעל קאָעפישענט פלאץ וואו איך האלט יעצט צו דעם עקספּאנענט פונעם בּיינוֺימיִעל פונעם נומער וואס איך האב געהאלטן מעיקרא. דאס אלעס גיי איך דערנאך מאָלטיפּלייען ביי די נומער וואו איך האלט
יעצט געהעכערט צום עקספּאנענט פונעם
בּערנוֺיליִ נומער פלאץ וואס איך זוך. אזוי גיי איך טוהן צו יעדעס נומער ביז איך קום אָן צום נומער וואס איך האב געהאלטן ביי מעיקרא, און דערנאך דאס אלעס צאמעדדן.
דערנאך, אזוי ווי פריער וואו איך האב אנגעהויבן פון 0 ביז׳ן
בּערנוֺיליִ נומער פלאץ וואס איך זוך און דיוויידעד 1 ביי איינס מער ווי די נומער וואו מ׳האלט כנ״ל, גיי איך נעמען די סומע וואס איך האב פריער באקומען פון צאמעדדן די גאנצע פריערדיגע פראצעדור, און דאס מאָלטיפּלייען, די זעלבע נומער נאכאמאל און נאכאמאל, ביי די אנגעהויבעכץ פון 0 ביז׳ן
בּערנוֺיליִ נומער פלאץ וואס איך זוך און דיוויידעד 1 ביי איינס מער ווי די נומער וואו מ׳האלט און אזוי ארויפגייענדיג, און
די אלע ענטפערס וואס איך באקום צאמעדדן צוזאמען. דאס וועט מיר געבן די געזוכטע
בּערנוֺיליִ נומער.
דאס איז די פארמולע דערפאר
(עס ווערט גערופן א דאפלטע סאָמעישׁאָן):
אן אינטרעסאנטע זאך מיט די
בּערנוֺיליִ נומערן איז אז חוץ דעם ערשטן [פלאץ] וואס איז 1/2 [קען זיין פאזיטיוו אדער נעגאטיוו], איז יעדעס
בּערנוֺיליִ נומער וואס איז אין אַן אַדד פלאץ אינעם סיִקווענס 0. די וואס זענען אין אַן איִווען פלאץ [חוץ די מקום פון 0 וואס דעמאלטס איז די נומער 1] זענען אלע [רעשׁאָנעל] פרעקשאנס. אנגעהויבן פון פלאץ 2 וועלכעס איז פאזיטיוו 1/6, איז די נעקסטע פרעקשאן נעגאטיוו, די נעקסטע פרעקשאן פאזיטיוו, די נעקסטע פרעקשאן נעגאטיוו, אא״וו.
יעצט, אז איך וויל וויסן די סומע פון עני אזא סארט סיריִס כנ״ל, לייג איך אריין די נומער אין
פאַוּלהאַבּער׳ס פארמולע. והיינו, אויב וויל איך וויסן די צאל פון א סיריִס אנגעהויבן פון א נומער ביז אן אנדערן געוויסן נומער וואו אלע נומערן אינצווישן ווערן עדדעד צוזאמען, און זיי אלע האבן דעם זעלבן עקספּאנענט, דעמאלטס ארבעט עס כזה:
איך נעם די נומער ביי וואס עס ענדיגט זיך און איך העכער דאס צום עקספּאנענט וואס איך בין דן אין, און איך דיווייד דאס ביי 1 מער ווי אט דעם עקספּאנענט. דערנאך לייג איך צו צו דעם האלב פון דעם נומער ביי וועלכעס עס ענדיגט זיך נאכ׳ן ווערן געהעכערט צו דעם עקספּאנענט. פון דעם אלעם באקום איך א נומער.
דערנאך, אנגעהויבן פון 2 און געענדיגט ביים נומער פונעם עקספּאנענט פונעם דיון, און ביי יעדעס נומער נעם איך די
בּערנאָלי נומער פון יענעם פלאץ-נומער און איך דיווייד דאס ביי די פעקטאָריעל פון יענעם [פלאץ-]נומער. דערנאך נעם איך די פעקטאריעל פון די עקספּאנענט און איך דיווייד דאס ביי דע פעקטאריעל פון 1 מער ווי די חילוק צווישן די עקספּאנענט און די נומער וואו איך האלט יעצט. דערנאך מאָלטיפּליי איך דאס ביי די נומער וואו איך גיי אריגינעל ענדיגן געהעכערט צו אן עקספּאנענט וואס איז איינס מער ווי די חילוק צווישן דעם עקספּאנענט פונעם עיקר דיון און די נומער וואו איך האלט יעצט. אזוי טוה איך ביי יעדן נומער, אנגעהויבן פון 2, ביז איך קום אָן צום נומער וואס איז די עקספּאנענט פונעם דיון, און איך עדד
דאס אלעס צאם. דערנאך שטעל איך צאם די נומער וואס איך באקום מיט׳ן נומער וואס איך האב באקומען פונעם פריערדיגן פּארגראף, און דאס גיבט מיר דעם ענטפער וואס איך האב געזוכט.
די פארמולע זעהט אויס אזוי:
די
בּערנאָלי נומערן קומען אויף אין אסאך מקומות במאטעמאטיקס.