קאווע שטיבל

ולגבי גראַנדיִ׳ס סיריִס, וואו ס׳איז בעצם שייך צו זאגן דערויף אז עס קאָנווערדזשד צו 1 ווי אויך אז עס קאָנווערדזשד צו 0 [ווענדענדיג ווי אזוי מ׳טוהט דרס גרוּפּן], איז אינטרעסאנט צוצוצייכענען אז דאס ברענגט צו צום איילענבערג-מאַזוּר שווינדל וואס ״ווייזט אויף״ אז 0 = 1. דאס איז דורך נעמען דעם גראַנדיִ׳ס סיריִס און דאס גרוּפּן און דערנאך עפּלייען דעם עסאָסיעטיוו פּראַפּערטי כזה: ‏מ׳קען צו דעם אפשר ווייטער צושטעלן דעם געדאנק דערפון בתוך טעאלאגיע אז ישות איז בעצם אַיִן וכן להיפך.

דאס גייט אביסל אין איינקלאנג מיט די געדאנק פון א טעלעסקאָפּינג סיריִס, וואו א (לעצטע) חלק פון איין טערמין קענסעלט אויס די ערשטע חלק פון די נעקסטע. ואשר על כן בלייבט נאר איבער דאס ערשטע חלק פונעם ערשטן און לעצטן חלק (ביי קאָנווערדזשענס) פונעם ״לעצטן״.

און אז מ׳האט דערמאנט די געדאנק פון גאָדעל׳ס טעארעם, וואס צייגט טאקע אויף די געדאנק פון אומעגליכקייט אלעס צו דערגיין בתוך א סיסטעם, שרייבט דער מאטעמאטיקער דר. דזשעימס סטיין אז עס איז יתכן אז עס איז דא א פּרוּף וואס צייגט אויף דאס אומעגליכקייט צו אויפווייזן אדער אפפרעגן מציאת הא-ל (איינמאל מ׳האט דעפינירט די פּראַפּערטיס פונעם מושג ״ג-ט״):

Both sides [theism and atheism] have been so busy trying to construct proofs supporting their case that it seems to me they have overlooked the obvious. Once the attributes of a deity are precisely defined, there may be a proof that it is impossible to prove the existence or nonexistence of such a deity. Alternatively, the deity hypothesis may possibly be shown to be independent of a set of philosophical axioms, adjoining either the deity hypothesis or its negation to those axioms leads to a consistent axiom set

בנוגע דאס געדאנק פון ״עקזיסטענץ״ לגבי ג-ט שרייבט דר. דוד ביאלע במשנתו של שלמה מיימון:

Using a classically Maimonidean argument, Maimon claimed that the statement "God exists" is no more meaningful than the statement "God does not exist." In this world, we mean by existence something that could or will go out of existence. Such a meaning cannot be applied to God; it is a category mistake, like saying "the wall does not see" (an example from Maimonides). The existence of God is beyond rational proof since the very concept of existence cannot be predicated of God. Since both belief and disbelief in God's existence are self-contradictory, the philosopher cannot be an atheist. But, by the same token, he or she cannot be a believer, at least not in the traditional sense of the word

ולגבי לימיטס (די געדאנק אין סיריִס) אין טעאלאגיע במשנתו:

Maimon’s God is the idea of perfection, the sum of all perfections, which, as Socher has shown, was the medieval idea of “the perfection of the soul” (shelemut ha-nefesh). Put differently — and in Maimonides’ language — God represents the unity of the intellect and the object of thought. Our understanding can never be identical to that of God, but we can grasp what it means to unite our intellect with the object of thought through mathematics. When we think of three straight lines whose ends are connected to each other such that the sum of their angles is 180 degrees, our thought and the triangle we have constructed through our thought are one and the same. Thus, when thought is constructive in this sense, it resembles in a limited way the thought of God

In doing so, we approach asymptotically, but do not ever reach, the infinite mind of God, a mind that does not exist in any worldly sense but instead exists as a regulative principle or a limiting concept. This language, drawn from the infinitesimal calculus of Leibniz and Newton, was one of Maimon’s innovations, since he wished to apply the most recent mathematics to philosophical reasoning. When, at the end of the nineteenth century, the neo-Kantian Jewish philosopher Hermann Cohen used calculus as the model for his own highly abstract idea of God as a “principle of origin,” he was reviving Maimon’s philosophy, whether he knew it or not

ועיין כאן כעין ענין זה ג״כ בענין לימיטס אודות מושג ה״משיח״ לפי דר. סטיווען שווארצטשיילד עפ״י הרמב״ם.

ועוד בנוגע דאס געדאנק פון קשר מאטעמאטיקס וטעאלאגיע האט חיים נחמן ביאליק געהאט געשריבן אין זיין גילוי וכיסוי בלשון:

הדבר הגיע לידי כך, שלשון האדם נעשתה כשתי לשונות, שנבנות זו מחרבן זו: לשון פנימית, לשון היחוד והנפש, שהעיקר בה, כמו במוסיקה, ה“איך”, לחוד - במדור השירה. ולשון חיצונית, לשון ההפשטה וההכללה, שהעיקר בה, כמו במתימטיקה, ה“מה”, לחוד – במחיצת ההגיון.

און דר. ביאלע איז דאס מסביר:

Distanced from its divine origins, we inherit language in its profane state in which only the husks remain, emptied of their original content. This is the conventional language of social interaction. It is also the language of mathematics, the domain of logic. Here, one cannot help thinking of Spinoza’s very different use of mathematical language. Where, for Spinoza, geometric proofs were the only language adequate to describe God, for Bialik, this language is by definition empty of all meaning beyond the conventional. Against a whole philosophical tradition that included Spinoza and Maimon, Bialik undercuts the claim of mathematics to convey necessary truth

און שפראך אליין, זאגט ביאליק, איז דאס מחיצה והפסק וואס איז דאס מכסה, און ער איז דאס מדמה אז עס איז מכסה פונעם תוהו פון ״כי לא יראני האדם וחי״. האט דאס ווייטער א קשר איינע צום צווייטן אז מ׳קען נישט ארויסברענגען דורך שפראך דעם געדאנק פון ״ג-ט״. ודומו סלה (וכידוע מהמו״נ, לדוגמא בח״א פ״נ).

די באקאנטע מאנדעלבּראָט סעט אין פרעקטעלס ווערט אויך אויסגעשטעלט דורך דעם מהלך פון קאנווערדזשענס לעומת דייווערדזשענס. עס ווערט צאמגעשטעלט (בקיצור נמרץ מאד מאד) אז איך האב א פאָנקשען פון:
x²+c
איך הייב אָן מיט x אלס 0 און פאר c וועהל איך א (קאַמפּלעקס) נומער. די נומער וואס איך באקום ארויס דערפון שטעל איך דערנאך אלס׳ן x און איך הייב אָן דעם שפיל נאכאמאל מיט׳ן דאס עדדן צו מיין c. די נומער וואס איך באקום יעצט שטעל איך דערנאך אלס x און עדד צו מיין c. אא״וו אא״וו. אויב דייווערדזשד עס און עס ווערט כסדר העכער און העכער, איז די c נישט קיין חלק פונעם מאנדעלבּראָט סעט. ווידער אויב קומט עס צו צו א ספּעציפישע נומער, דאן איז די c יא א חלק פונעם מאנדעלבּראָט סעט.

ווען מען גרעפט דאס אויפ׳ן קאַמפּלעקס פּלעין (אויך פון וואס ריעמאן האט גע׳ארבעט אויף לגבי מעניפאלדס) זעהט עס אויס אזוי מיט סעלף-ריפּיִטיִנג פרעקטעלס: ***

דאס איז וויאזוי דר. פּאָל וואָקער איז מסביר דעם דאָבּל נעגעישען געדאנק אין טעאלאגיע פונעם פרסי'שען פילאזאף בזמן הגאונים אבוּ יאקוב אַל-סידזשיסטאַני: און ווי דר. פּיִטער עדעמסאן זאגט אויף דעם/אים: ***

דר. סטיין נוצט זיין אויבן-דערמאנטן געדאנק פון גאָדעל׳ס טעארעם אז עס איז אויך יתכן עפי״ז אז עס איז אומעגליך צו טרעפן א טעאריע פון אלעס אין פיזיקס וואס גייט פאראייניגן עמפירישע געפינסן ומדע אא״וו אונטער איין טעאריע. ענליך זאגט דער ביאלאגיקער דר. יוּדזשיִן קוּנין לגבי אַן אלגעמיינע ברייטע טעאריע פון עוואלושאן בתוך ביאלאגיע:

The computational biologist Eugene Koonin thinks people should get used to theories not fitting together. Unification is a mirage. “In my view there is no – can be no – single theory of evolution,” he told me. “There cannot be a single theory of everything. Even physicists do not have a theory of everything.”

‏ובענין רעליגיע מיינט דאס אבער נאך ווייט נישט א ״גאַדידיט״ תירוץ (וואס איז נאך ווייניגער פארשטענדליך ואפילו ממבט הטעאיסט עצמו, המאמין בעיקר הג׳ של הרמב״ם; ״בורא ומנהיג״ איז אזא סארט לשון מושאל); מ׳דארף פשוט דאס משפר זיין בתוך דעם סייענטיפישן פרעימווארק - אזוי ווי די פּראגרעס אין סייענס איז אלס צוגעגאנגען און וועט (האפענטליך) אלס צוגיין.

דר. פּאָל פרענקס שרייבט במשנתו של שלמה מיימון:

this criticism enabled a deeper validation of Maimonides: formal synthesis was exemplified by mathematical construction, in which the intellect, the formal activity, and the constructed object were one. Mathematics was the paradigm of infinite intelligibility, in which we accomplished something like creatio ex nihilo and were similar to God

די ענציקלאָפּעדיע בּריטאַניקא איז מסביר קאַנשׁעסנאס במשנתו של שלמה מיימון (עפ״י קאנט׳ס געדאנק פון נומענאן):

It was not till 1788 that he made the acquaintance of the Kantian philosophy, which was to form the basis of his lifework, and as early as 1790 he published the Versuch über die Transcendentalphilosophie, in which he formulates his objections to the system. He seizes upon the fundamental incompatibility of a consciousness which can apprehend, and yet is separated from, the “thing-in-itself.” That which is object of thought cannot be outside consciousness; just as in mathematics √-1 is an unreal quantity, so “things-in-themselves” are ex hypothesi outside consciousness, i.e. are unthinkable

דר סקאַט עראנסאן שרייבט:

As Jordan Ellenberg, a mathematician at the University of Wisconsin, wrote, a dirty secret in mathematics is that many unsolved problems have a similar flavour: they’re less about mysterious coincidences than about the lack of them

Take, for example, the Twin Primes Conjecture, which holds that there are infinitely many pairs of prime numbers separated by 2 (such as 3 and 5, or 11 and 13). Ellenberg explains that, for this conjecture to be true, there doesn’t need to be any mysterious ‘force’ pulling primes together; there just needs not to be a mysterious force pushing them apart. Or take the Riemann Hypothesis, which states that the infinitely many non-trivial roots of a certain complex function all lie on a single line. When it’s stated that way, the hypothesis does sound like a mystery. Why should infinitely many numbers all happen to line up like that?

The mystery lessens once you realise that each zero of this function encodes global information about the distribution of prime numbers – and a single zero off the line would represent infinitely many prime numbers clumping together in astronomically improbable-seeming ways. So, if you like, one mysterious pattern has to be there to prevent a second pattern that would be even more mysterious

ער שרייבט אז דאס איז בנוגע מאטעמאטיקס בכלליות: עס האט אַן אינטוּאיטיוו סענס (פאר דער וואס פארשטייט דאס) וואס דאס פאלגט נאך; עס איז נישט בעצם ״מיסטעריעז״. ועכ״כ אז בעצם האט מען זיך נישט צו שרעקן פאר גאָדעל׳ס טעארעמס וועלכע עפּלייען נאר זעלטן. און אט דאס איז א מיסטעריע וכידוע מדר. יוּדזשיִן וויגנער (לגבי מאטעמאטיק׳ס שטארקע קשר לפיזיקס).

אין מאטעמאטיקס איז דא צוויי געדאנקן פון א ״רעגולאר נומער״:

1). א נומער וואס קען דיוויידען 30 אדער 60 (די נומערן וואס קומען ארויס פון געבן עקספּאנענטס צו 30 אדער 60) אָן קיין רימעינדאר. והיינו, א נומער וואס אירע פּריים דיווייזארס פון וואס די נומער איז צאמגעשטעלט זענען נאר 2, 3, און 5.

2). א נומער וואס איך קען נישט צוקומען דערצו דורך צאמעדדן ווייניגער ווי די צאל פון די עצם נומער פון די נומערן אונטער דעם. למשל די נומער 1 איז א ״רעגולאר נומער״ ווייל מ׳קען נישט צוקומען צו 1 דורך איין 0 וואס איז אונטער דעם. ווי אויך איז 2 ״רעגולאר״ ווייל מ׳קען נישט צוקומען דערצו דורך צאמעדדן ווייניגער ווי 2 נומערן וואס זענען אונטער דעם. אין מעטאפיזיקס צייגט דאס אויף דאס שוועריקייט פון ווי אזוי קומט פון ״אַיִן״ [״0״] א ״יש״ [״1״]. ווי אויך אז ווי אזוי קומט פון אַן ״אחד הפשוט״ [״1] א ״ריבוי״ [״2״] (ועיין בעיקרים מאמר ב פי״א).

לייבניץ האט גע׳טענה׳ט אז פון גראַנדי׳ס סיריִס, אויב זאג איך אז דאס קאַנווערדזשד צו 1 אדער 1/2, דאן זעהט מען דאך ווי פון 0 ווערט 1 (אדער עכ״פ 1/2). מ׳קען דאך באטראכטן די סיריִס ווי (1-1)+(1-1)+(1-1) אא״וו, וואס באדייט דאך דאס זעלבע ווי 0+0+0 אא״וו [אַן אַיִן], און פונדעסטוועגן קומט דאס אָן צו א ״יש״.

דר. פּיִטער עטקינס זאגט אז בכלל קען מען דאך צוטיילן 0 אין צו פאזיטיוו 1 און נעגאטיוו 1; עס איז דאך 0=1-1. און 0 באדייט וואו עס איז נישטא קיין זמן בכלל. פאזיטיוו 1 גייט באדייטן וואו צייט גייט פאראויס און נעגאטיוו 1 גייט באדייטן וואו צייט גייט צוריקצווועגס (פון אונזער מבט). וממילא איז די ״יש מאין״ צושטאנד געקומען ווען די ״0״ האט זיך צוטיילט אין צו 1 און 1-, ווי אין איין יוּניווערס גייט צייט פאראויס און אין די אנדערע צוריקצווועגס. (דזשאַן אָפּדייק ברענגט דאס אויך צו.)

‏@מתבודד האט געשריבן:

מתבודד האט געשריבן:דער בעל התניא פלעגט טאקע רופן די וועלט אַן ”אַיִן מִיֶשׁ” און נישט קיין יֶשׁ מִאַיִן, כידוע.

דאס שטימט יא מאטעמאטיש און לאגיש?...

אויב דעפינירט מען אַן ״אינווערס״-רעגולאר נומער אלס א נומער וואס מ'קען נישט צוקומען דערצו דורכ׳ן סאָבּטרעקטן כאטש אזויפיל נומערן ווי די נומער וואס זענען העכער/גרעסער ווי איר, דאן איז 0 נישט אזא סארט נומער ווייל מען קען יא: 3-2-1=0.

די ראמאנוזשאן טאַוּ פאָנקשען איז ווען איך נעם א נומער און איך געב דערצו אַן עקספּאָנענט פון 1. דערנאך, די נומער וואס איך באקום, וואס איז דאס זעלבע נומער, נעם איך דאס אוועק פון 1, און איך העכער וואס איך באקום צו אַן עקספּאָנענט פון 24. איך העכער דערנאך דעם אריגינעלן נומער צו אַן עקספּאָנענט פון 2 און איך טוה איבער דעם זעלבן שפיל הלאה והלאה העכערענדיג דעם עקספּאָנענט, און איך מאָלטיפּליי אט די גאנצע סיריִס צוזאמען. דערנאך מאָלטיפּליי איך וואס איך באקום ביים אריגינעלן נומער. סרינוואסא ראמאנוזשאן האט קאָנדזשעקטשורד אז טאמער איז די נומער איך וועל אויס א פּריים, דאן וועט די פאָנקשען פאר דעם פּריים נישט זיין מער ווי אויב איך נעם די פּריים און געב עס אַן עקספּאָנענט פון 11 און דערנאך נעם איך די סקווער-רוּט פון וואס איך באקום, און איך מאָלטיפּליי דאס ביי 2. עפ״י מאטעמאטישע לומדות האט דאס א שייכות צום ריעמאן היפאטעזיע.

עס קומט אויך אויס אז טאמער געב איך נישט קיין וועליוּ פאר q און איך לאז עס, און אזוי טוה איך מאכן די מאָלטיפּליקעישאן (אזוי אז עס ווערט א פּאַלינאָמיעל), דאן גייען די פראדוקט פון די קאָעפישענטס, והיינו די נומערן, פון יעדעס טערמין צוזאמען זיין די קאָעפישענט פון די פראדוקט פון זייער טערמין פלאץ. מיינענדיג, למשל די קאָעפישענטס פון די צווייטע און דריטע פלאץ ווען איך מאָלטיפּליי זיי צוזאמען, וועט זיין די קאָעפישענט פון די זעקסטע פלאץ, וואס צוויי מאל דריי איז זעקס.

‏דא האט @הקטן געשריבן:

הקטן האט געשריבן:איך האלט, למשל, דאס אן אשכול בנוגע רימאן זעטא געט גארנישט צי צים פלאץ

אין די קאנטעקסט דארט איז עס צוגלייכן די דאזיגע אשכול איבער (הויכע) מאטעמאטיקס צו די parochial שאלה ״וועמענ׳ס רבי איז די גרעסטע?״ אדרבה קוקסט נאך. סתם אזוי וואלט איך עפּלייט דאס פּרינציפּ פון טשעריטי און געזאגט אז ער מיינט ענליך צו @הבל וריק׳ס טענה פריער, אז דאס איז דאך שטארק חכמה און לאו כל מוחא סביל דא. אבער גיין זאגן ״דאס געבט גארנישט צו״ און שטעלן דעם שמועס דא אויף דעם זעלבן לעוועל פון זיך טענה׳ן ״וועמענ׳ס רבי איז גרעסער״, איז נישט קיין סימן אויף חכמה, מילד גערעדט, און דארף צו פארשעהמען די חברים דא. פונעם פּערספּעקטיוו פון א קינד און א סכל זענען זיי טאקע אייניג.

און אזוי ווי איך האב גע׳ענטפערט איז דאך אט דאס די געדאנק: אויף די (ועכ״פ איינע פון די) אינטעלעקטשואלע forum ביהדות החרדית פאסט עס זאלן זיין אזעלכע סארט אשכולות ווי מ׳רעדט ארום וועגן דעם.

כידוע, איז מאטעמאטיקס די נענסטע מ׳קען צוקומען צו ״אמת״, ועיין באשכול טענה. (ואיה״נ אז דאס האט אויך די שוואכקייט פונעם מונכהאַוּזן טריילעמאַ (וואס איך בין מסביר אין מיין ארטיקל על נושא אמונה) אבער דאס איז סתם אזוי לגבי ״אמת״ בכלליות. ועיין בחתימתי בכלל, פון וואס @הקטן אליין האט טאקע אפגע׳חוזק׳ט. אבער בתוך זה איז דאס אבער דאך די נענסטע, ופשוט.) ואולי עפי״ז קען מען טאקע זאגן א רמז בסוף סוטה לגבי עיקבתא דמשיחא ״וחכמות סופרים תסרח ויראי חטא ימאסו והאמת תהא נעדרת״. והיינו, בעיקבתא דמשיחא איז דאס׳ן משווה זיין ״ווער איז גרעסער און ווער איז קלענער״ פון די סופרים ויראי חטא אויפ׳ן זעלבן מדריגה ווי חשיבות ״אמת״ ומאטעמאטיקס ווייל דאס איז נעדרת.

אין קורצן, נעבעך. (און דאס איז שוין פון איינעם וואס נעמט זיך אָן פאר אמונה בהשטיבל. אז מ׳פרעגט מיר איז דאס א חילול ה׳ און ברענגט אראפ די ווערט פון אט די אמונה בעיני החכמים.

שוין. כלום מתקנא אלא חכם בחכם. און עס איז טאקע מן הראוי צוצוצייכענען צו וואס @אדנירם האט געשריבן בסוף תגובה זו.

.

איזי איזי...
ווען איינער זאל ווען קאיפען שטיקער תנ"ך דא, וואלט איך אויך געשריבן דאס וואס איך האב געשריבן

ס'איז היינט אן אפענע וועלט און ווער ס'וויל לערנען חכמה האט ב"ה אווי צי גיין


דיין Ad hominem ארגיאמענט געט אויך נישט קיין סך צי

הקטן האט געשריבן:ווען איינער זאל ווען קאיפען שטיקער תנ"ך דא וואלט איך אויך געשריבן דאס וואס איך האב געשריבן

מ'טוהט דאס דאך טאקע דא אבער בהסבר (ולדוגמא אפאר פון @קאך_לעפל'ס אשכולות) - איך געדענק נישט דו זאלסט האבן געזאגט אזאנס אויף זיי. און אט דאס פרוביר איך צו טוהן פונקט אזוי ביי די נושא, און אזוי ווי @פארוואס? האט געטוהן אין זיינע מאטעמאטישע אשכולות וואס ער האט "געקאַפּיט". די חילוק איז אז כנראה יענץ פארשטייסטו און דאס נישט. (ווי אויך האסטו אליין נישט געהאט די טענה אויף מיין אשכול איבער טערמאדינאמיקס, וואס איז פונקט אזוי ״געקאַפּיט״, און אפילו מיטגעהאלטן דארט.)

הקטן האט געשריבן:דיין Ad hominem ארגיאמענט געט אויך נישט קיין סך צי

קיימתי בך עם עקש תתפל, דכך דרכך. ובפרט אז עס געבט יא צו צו פארוואס איך בין דיר נישט דן לכף זכות מיט'ן פּרינציפּ פון טשעריטי וכדכתבתי. איך שטיי ביי יעדעס ווארט איך האב געשריבן.

צו ענדיגן, צו ״קאַפּיען״ אזוי ווי דו האסט ליב צו זאגן אויף אנדערע, איז דיין אנטווארט דא:

הקטן האט געשריבן:אויבערפלעכלעך עס-יאזעל

איך ווייס נישט פין וועלכע אשכול דו רעדסט וואס ברענגט שטיקער תנ"ך תגיבה נאך תגיבה אן קיין דיסקאשען בעק-ענד-פארד פין אנדערע חבירי השטיבל.
אויב אזא אשכול וואלט ווען געווען אין טאפ פין אקטיווע אשכולות וואלט איך ווען מן הסתם יענץ געניצט פאר א משל (די אשכול, און אנדער אזאלכע אשכולות איז דאך נישט היינט געבוירען, און איך האלט וואס איך האלט, שוין א לאנגער צייט, אן דעם וואס איך זאל זאגן א ווארט דערוועגן, וואו לאנג דאס מאכט דיך גוט פילען - איי דאנט גיוו עי, מנלנ"ז, האט)

צי איך פארשטיי יא צי ניין איז מיר שווער צי ענפערן ווייל ווען איך לערנען מאטעמאטיק האב איך בעסער ליעב צי ליינען און ענגליש
ליבי אומר לי דאס איז אזוי ביי אסך, אנ-לעס ס'ווער א שמוס פין זה אומר בכה וזה אומר בכה

איז טוישסטו (עד האַק) פון א פראבלעם פון ״קאַפּיען״ צו פשוט א פראבלעם אז די עולם האלט נישט מיט. אין אנדערע ווערטער, האלטסטו אזוי ווי @cictim. איך האלט נישט אזוי וכ@העניך שם. און אזוי ווי @מונטסורי האט געשריבן דא:

מונטסורי האט געשריבן:למעשה האלט מיר יעצט אינמיטען דורכלערנען דעם תגובה פון @מי אני און דאס קאפ שווינדעלט, גענוג געווען פאר איין יום טוב, גיימיר מאכן אייער שפייז. ומכאן הקריאה יוצאת צו @מי אני חלילה נישט מיד צו ווערן, אפילו עס קוקט אמאל אויס אז דער עולם שלאפט ביים שיעור, ביום מן הימים וועט איינער ווער דא אריינפאלן, פרובירן צו ליינען און אפשר א לייק טון.

ווי אויך איז עס לענ"ד סתם אזוי א סארט סורווייווערשיפּ בּייעס זיך נאר וויסענדיג צו מאכן און רעכענען דאס "וואס געבט צו צום שטיבל" לפי די רעאקציעס, די "בּעק ענד פאָרט", וואס מ'זעהט דאס באקומט, און מ׳נעמט נישט אין באטראכט די וואס ליינען דאס סתם וואס זיי זעהט מען נישט. מ'זעהט אז רוב פון די וואס שרייבן זיך איין מיט זייער ערשטע הודעה אין די "שלום עליכם" אשכול זאגן אז זיי ליינען שוין דא אלס געסט א לענגערע וויילע, און ווי @מיימון האט דארט ארויסגעברענגט שרייבן רוב פון זיי נישט ווייטער קיינע תגובות, הגם זיי זעהן אויס ווי חכמים. אבער כנראה ליינען זיי אבער פארט די אשכולות און ארטיקלען. (איך בין א קעיס-אין-פּוינט: איך האב נישט רעאגירט אין יענעם אשכול איבער "ווער איז גרעסער" אבער איך האב פארט געזעהן דיין נארישע תגובה.) אין אנדערע ווערטער, ס'איז שטארק יתכן ו"לבי אומר לי" אז די וואס ליינען דאס בסתם, צי אלס סתם גאסט צי אלס איינגעשריבענע באניצער וואס ראאגירן נישט און לייקן נישט, זענען די רוב כנגד די וואס וואלטן ווען געדארפט רעאגירן און רעאגירן אויף אנדערע אשכולות. און @יואב האט זיך טאקע אפגערעדט דערויף אז היתכן מער מענטשן האלטן נישט ממש אקטיוו מיט מיט די סארט טעמעס. עס וואלט טאקע געפאסט פאר'ן עם חכם ונבון.

ולסיים, זאלסט מיר מוחל זיין (אדער נישט) אבער צו דעניגרעיטן אשכולות וואס זענען למעשה אינהאלטסרייך און איבער חכמה און דאס נישט עפּרישיעיטן, צייגט אז דער מענטש וואס דעניגרעיט דאס איז נישט קיין חכם, ועיין ברבינו יונה בריש פ"ד באבות. און ווי געזאגט איז עס א שאד וויבאלד עס זענען דא די וואס האלטן דיר פאר א ידען וכו׳ און אלס איינער וואס קען ענטפערן אויף עניני אמונה. איך וואלט געזאגט א סארט (אבות א יא) ״חכמים הזהרו בדבריכם״ אבער איך האלט נישט אז דאס עפּלייט, וכנ״ל. וממילא לגבי ״וואס דו האלטסט״, איז צו נוצן די לשון פונעם מרדכי (ע״ז תתנד, והובא בטו״ז יו״ד סימן צח ס״ק ו): ״דעת טפשין/שוטים אינו כלום״ (און דאס איז טאקע אינעם קאנטעקסט פון נישט וויסן ווי אזוי און נישט קענען "רעכענען" ששים...). וידוע ד״קטן״ לאו בן דעה הוא (לדוגמא בחגיגה ב: בגיטין כג. ובמנחות צג.).

מיין זיך אפגעבן אין די לענג מיט דיינע דברי בלע איז אפשר א ביישפיל פון קאָנינגהעם׳ס געזעץ, וואס קיינער האט טאקע נישט רעאגירט דערויף דארטן וואו איך האב עס צוגעברענגט, אבער דו אליין האסט דאס טאקע געליינט און געלייקט. (ואולי איז דאס אויך א ביישפיל פונעם פריער-דערמאנטן בּרענדאליני׳ס געזעץ.)

אז מ׳האט פריער אראפגעברענגט דע מארגענ׳ס געזעצן אין לאגיק, איז קען מען דאס נוצן אויף אויפצוווייזן קעגן אנסעלמ׳ס אנטאלאגישע ארגומענט. ווי באקאנט, ארבעט זיין ארגומענט אז מ׳דעפינירט ״ג-ט״ אלס די being פון וואס גרעסער/מער ווי דעם קען מען זיך נישט מצייר זיין בכלל. און די געדאנק קען מען זיך דאך מצייר זיין במחשבה. אויב אבער עקזיסטירט דאס נישט דאן איז דאך יא שייך עפעס מער/גרעסער, והיינו א being וואס עקזיסטירט אויך און דאס איז א סתירה צו וואס מען האט זיך ממש פריער מגדיר געווען. אין אנדערע ווערטער, זאגן ״ג-ט [עפ״י ההגדרה הנ״ל] עקזיסטירט נישט״ איז א סתירה מיניה וביה.

כידוע האט שוין דער כומר גאנילו פון מאַרמאָטיער געפרעגט דערויף בשעתו אז מ׳קען דאך נוצן דאס זעלבע לאגיק אויף אויפצווויייזן אז די מערסטע פּערפעקט אינזל עקזיסטירט בע״כ, וכדומה. אויף וואס אנסעלם האט גע׳ענטפערט אז די געדאנק פון מערסטע/גרעסטע פּערפעקשאן ליגט אין די הגדרה פון ״ג-ט״ משא״כ ביי ״אינזל״ וכדומה.

קאנט האט געפרעגט אויפ׳ן הוכחה אז עס איז נישט שייך צו זאגן אויף ״עקזיסטענץ״ אז עס איז א פּרעדיקעט וואס עפעס ״פארמאגט״ אדער נישט, וממילא דן צו זיין דערויף צו די עפעס האט דאס ״אויך״ צי נישט. צו זאגן אז ״דאס-און-דאס עקזיסטירט נישט״ איז נישט צו געבן ״נישט-עקזיסטענץ״ צו עפעס אַן ענטיטי - עס איז איידער צו זאגן אז גארנישט טוהט באפרידיגן די-און-די הגדרה.

מ׳קען דאס זעהן עפ״י דע מארגענ׳ס געזעץ אז עס איז נישט א סתירה מיניה וביה אפילו ווען מ׳לייגט אריין ״עקזיסטענץ״ בפירוש:

לאז ג׳ = ג-ט

לאז פּ׳ = אינפיניטלי פּערפעקט

לאז ע׳ = עקזיסטענץ

‏∀x[גx↔(פּx&עx)]
מיינענדיג,
‏עפעס איז ג-ט אויב און נאר אויב [iff] די עפעס איז אינפיניטלי פּערפעקט און די עפעס עקזיסטירט

דאן צו זאגן ״עס איז נישטא קיין ג-ט״ איז דאס זעלבע ווי זאגן:
‏~∃x[(פּx&עx)]
מיינענדיג,
‏עס איז נישטא קיין עפעס אזוי אז די עפעס איז אינפיניטלי פּערפעקט און די עפעס עקזיסטירט

און עפ״י דע מארגענ׳ס געזעץ איז דאס די זעלבע ווי זאגן:

‏∀x[(~פּx) אדער/v (~עx)]
מיינענדיג,
‏פאר יעדעס עפעס, אדער איז די עפעס נישט אינפיניטלי פּערפעקט אדער די עפעס עקזיסטירט נישט

מ׳קען זעהן אז עס איז נישטא קיין סתירה דערין אין די לעצטע זאץ.

און אז מ׳האט דערמאנט דער לאגיקער דר. קורט גאדעל אינעם אשכול (ובענין טעאלאגיע), האט ער געמאכט א ווערסיע פונעם אנטאלאגישן ארגומענט עפ״י מאָדעל לאגיק - א לאגיק וואס ארבעט ארום מיט ״מוכרח, מעגליך, אדער אומעגליך״. ווי דער טעאלאג דר. עלווין פּלענטינגא איז דאס מסביר (אין קורצן) אז א ״great being״ באדייט אז עס וואלט געווען “great” נישט קיין חילוק ווי אזוי אימער אומשטענדן וואלטן זיך ווען אויסגעשטעלט. א “maximally great being״ באדייט אז דאס איז א “great being״ אין יעדעס מעגליכע וועלט [״וועלט״ אין איר פילאזאפישן/לאגישן באדייט]. אויב אזא being עקזיסטירט בכלל, עקזיסטירט דאס בהכרח אין יעדעס מעגליכע וועלט; עס איז דאך נישט קיין אפשרי בעצם הגדרתה. יעצט, אפילו דער אטעאיסט איז מודה אז די “maximally great being״, והיינו ״ג-ט״, איז (לאגיש) ״מעגליך״. אבער דאס באדייט דאך דאס זעלבע ווי זאגן אז אין עפעס א מעגליכע וועלט איז דא א ג-ט. און אויב איז דאס דא אין איין מעגליכע וועלט איז דאס דא בהכרח אין יעדעס מעגליכע וועלט וכנ״ל. (דאס האט נישט קאנט׳ס פירכא וויבאלד די געדאנק דא איז נישט ״עקזיסטענץ״ ווי איידער ״הכרח׳דיגע עקזיסטענץ״.) ‏דא הא׳מיר אראפגעברענגט אז אפילו אויף דעם זענען דא פירכות.

לגבי ראמאנוזשאן סאָמעישאן קען מען ״אויפווייזן״ אז די סיריִס פון:
1+2+3+4…
איז 1/12- אויב נעמט מען אָן אז גראַנדי׳ס סיריִס קומט אויס צו 1/2. והיינו, איך מאך א סארט גראַנדי׳ס סיריִס וואס טוישט זיך פון ״+״ צו ״-״ אבער וואקסט מיט אַן אבסאלוט נומער כזה:
1-2+3-4+5…
דערנאך פרעג איך וואס איז די סומע פון צוויי מאל די סיריִס: ווען איך עדד די סיריִס צו זיך. אבער וויבאלד דאס איז דאך אַן אינפיניט סיריִס, איז ווען איך לייג איינס צו צום צווייטן קען איך דאך בעצם ארויפרוקן די נומערן מיט איינס (דער אמת לאמיתו איז אז מ׳קען דאס נאר טוהן טאמער זיי זענען אַבּסאלוטלי קאָנווערדזשענט). מיינענדיג, עס וועט אויסזעהן אזוי:
1-2+3-4+5…
0+1-2+3-4…
און אזוי אויסשטעלן די וועליוּס און יעדעס איינס אראפרעכענען פון די נומער גראד העכער איר. ווי מ׳קען זעהן וועט דאס אויסקומען צום געהעריגן גראַנדי׳ס סיריִס וואס מ׳זאגט איז דאך 1/2. דאס איז אבער געווען צוויי מאל די סיריִס, וממילא איז אט די סיריִס קומט אויס צו האלב דערפון וואס דאס איז 1/4.

יעצט סאָבּטרעקט איך די נייע סארט גראַנדי׳ס סיריִס, וואס איך ווייס איז 1/4, פון פונעם (באמת דייווערדזשענט ערשטע סיריִס כזה:
1+2+3+4+5…
1-2+3-4+5…
ווי אָנגערירט אין די אשכול ווען מען סאָבּטרעקט א נעגאטיוו נומער פון עפעס איז כאילו איך עדד דאס פארקערטע. צב״ש, 1 מיינוס נעגאטיוו 1 באדייט 1 פּלאָס פּאזיטיוו 1. עפי״ז קען מען זעהן אז סאָבּטרעקטן די סיריִס פונעם ערשטן געבט:
0+4+0+8+0+12…
עס איז א פּעטערן פון נאך יעדעס 0 אינעם סיריִס וואקסט עס ביי 4. איך קען איגנארירן די 0׳ס און אז איך דיווייד די גאנצע סיריִס ביי 4 איז עס דאך די אריגינעלע סיריִס פון:
1+2+3+4…
ווייס איך אז די אריגינעלע סיריִס מיינוס די סיריִס וואס קומט אויס צו 1/4 איז 4 מאל אט די אריגינעלע סיריִס:
S-1/4=4S
אז איך סאַלוו פאר S קומט דאס אויס צו 1/12-.

עס זעהט אויס ״אילעגאל״ אבער למעשה טרעפט מען דאס אין פיזיקס. ‏דא, ווי דר. עדמונד קוֺיפּלענד איז דאס מסביר, שרייבט איינער: אז מען מאכט די אריגינעלע סיריִס הנ״ל נאר מיט יעדעס נומער אינעם סיריִס האבענדיג אַן איִווען עקספּאנענט איז די ראמאנוזשאן סאָמעישאן דערפון 0. אויב געבט מען עס אַן אַדד עקספּאָנענט, דעפינירט אלס איינס ווייניגער ווי 2 מאל א געוויסע נומער, דאן גייט די ראמאנוזשאן סאָמעישאן דערפון זיין די נעגאטיוו פון די בּערנאָלי נומער פון די פלאץ פון אט די 2 מאל א געוויסע נומער [אינעם בּערנאָלי נומער סיִקווענס], דיוויידעד ביי 2 מאל די געוויסע נומער. (ווען די עקספּאנענט איז א קיוּבּ, 3, דאן איז דאס למשל 1/120.)

דר. עדווארד פרענקעל טענה׳ט אז די ראמאנוזשאן סאָמעישאן לומדות איז די זעלבע סארט ״אילעגאל״ וואס האט בכלל געגעבן די נומער i פאר אַן איִווען-רוּט פון א נעגאטיווע נומער. און ער זאגט דאס איז אפילו ענליך צו ווען מען איז אויפגעקומען מיט ״אילעגאלע״ אירעשאנעל נומערן.

ווי געזאגט איז אויף גראַנדי׳ס סיריִס באקומט מען דורך די סעזאַראָ סאָמעישאן א סארט קאָנווערדזשענס צו 1/2. דאס ארבעט דורך דעם אז ביז יעדעס נומער אינעם סיריִס נעם איך די עוורידזש פון אלע נומערן צאמגערעכענט ביז אהין. די עוורידזש וואס קומט אויס דאס מערסטע, דאס גייט זיין מיין סומע דא. די לומדות ארבעט ביי געוויסע סארט דייווערדזשענט סיריִס. עס ארבעט אויך ביים צווייטן סארט סיריִס הנ״ל אויפצוווייזן אז עס איז 1/4. עס ארבעט אבער נישט ביים סיריִס פון:
1+2+3+4…
צו צייגן אז דאס איז 1/12-. דער מאטעמאטיקער דר. בּוּרקאַרד פּאָלסטער איז ברוגז אויף דעם חשבון הנ״ל… (יענעם חשבון קומט פונעם פיזיקער דר. אנטאני פּאַדיִאַ.) דר. פּאָלסטער ברענגט ארויס אז טאמער טוישט מען א משהו די ריעמאן זעטאַ פאָנקשען אז אנשטאטס נאר ״+״ האלט עס זיך אין איין טוישן מיט ״-״ ביי יעדעס צווייטע, דאן איז דאס די דיריכלעט עטאַ פאָנקשען; נאטירט אלס *ζ מיט א שטערענדעל אויבן (אדער מיט η.

אויב איך געב א 0 פאר׳ן s פון דעם דיריכלעט עטאַ פאָנקשען גייט דאס זיין גראַנדי׳ס סיריִס. און טאמער געב איך פאר s א וועליוּ פון 1- דאן איז דאס די צווייטע סארט גראַנדי׳ס סיריִס הנ״ל.

ער ווייזט אויף דאס אז עס איז 1/12- דורכ׳ן סאָבּטרעקטן די דיריכלעט עטאַ פאָנקשען פונעם ריעמאן זעטאַ פאָנקשען. עס קומט אויס אז יעדעס אַדד פלאץ וועט זיין 0, וואס איך קען איגנארירן, און יעדעס איִווען פלאץ האט א 2 אינעם נוּמערעיטאר און די דענאַמינעיטאר וואקסט מיט 2 (און האט די s עקספּאָנענט אויף זיך). אז איך דיווייד דאס אלעס ביי 2 איבער 2 מיט דעם s עקספּאָנענט איז עס דאך די געהעריגע ריעמאן זעטאַ פאָנקשען. אז מ׳סאַלווט דאס אלגעברעאיש קומט אויס אז די ריעמאן זעטאַ פאָנקשען איז דאס זעלבע ווי די דיריכלעט עטאַ פאָנקשען דיוויידעד ביי וואו איך האב אוועקגענומען פון 1, 2 דיוויידעד ביי 2 וואס האט די עקספּאָנענט פון s. און אז איך געב פאר s די וועליוּ פון 1- דאן איז דאך דאס ביים כנ״ל די צווייטע סארט גראַנדי׳ס סיריִס, וואס דאס ווייס איך דאך איז 1/4 ביים דיריכלעט עטאַ פאָנקשען, און ביים ריעמאן זעטאַ פאָנקשען איז דאס דאך:
1+2+3+4…
און אז איך סאַלוו עס יעצט קומט דאס אויס צו 1/12-. ועפי״ז קומט אויס אז טאמער געב איך פאר s א וועליוּ פון 0, וואס דאן איז דאך דאס די געהעריגע גראַנדי׳ס סיריִס כנ״ל, דאן גייט דאס אויסקומען צו 1/2-. (און דאס אז ביי יעדעס נעגאטיוו איִווען וועליוּ איז דאס וואס עס געבט ארויס 0, דאס זענען דאך די ״טריוויעל״ 0׳ס.)

‏דאס איז ראַמאַנוּזשאַן סאָמעישאן.

ער ענדיגט צו אינטרעסאנט אז טאמער איך טוה ביי די סיריִס פון:
1+2+3+4…
טוישן יעדעס נומער אין דעם לויט׳ן צאמרעכענען אלע נומערן ביז אהין:
1,3,6,10…
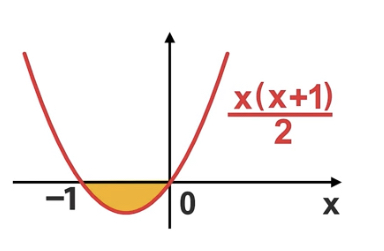
דאן איז דאך די פארמולא דאס צו וויסן ביז א געוויסע נומער, אזוי ווי קאַרל פרידריך גאַוּס האט אויפגעוואוזן אלס קינד, יענע נומער טיימס איינס מער ווי יענע נומער און איך דיווייד דאס ביי 2. אויב מיט ״יענע נומער״ מיין איך x, אזוי ווי אין אלגעברא בכלליות, און איך גרעף דאס, זעהט דאס אויס כזה. און די עריע אין די קוּרוו אונטער די x עקסיס [וואו ס׳איז געל] איז 1/12-.

לגבי סיִקווענסעס איז אינטרעסאנט צוצוצייכענען צו מוֺיסנער׳ס טעארעם. דאס זאגט אז איך קען צאמשטעלן א סיִקווענס פון
1,2,3,4,5…
וואו יעדעס נומער האט די זעלבע עקספּאָנענט דורכ׳ן טוהן כזה: למשל, אויב וויל איך וויסן וואס גייט זיין די סיִקווענס ווען יעדעס נומער האט אַן עקספּאָנענט פון 2, דאן נעם איך צום ערשט ארויס פון דעם געהעריגן סיִקווענס פון נומערן איינע נאך דאס אנדערע [אָן קיין שום עקספּאָנענט] יעדעס צווייטע נומער:
1,3,5,7,9…
דערנאך טויש איך יעדעס נומער אין דעם סיִקווענס לויט די סומע פון אלע נומערן וואס קומען בעפאר ביז אהין:
1,4,8,16,25…
דאס איז דאך:
1²,2²,3²,4²,5²…

אויב וויל איך דאס טוהן פאר, צב״ש, אַן עקספּאָנענט פון 4, דאן צום ערשט נעם איך אוועק יעדעס פערטע נומער אינעם סיִקווענס. דערנאך טויש איך יעדעס נומער אין דעם סיִקווענס לויט די סומע פון אלע נומערן וואס קומען בעפאר ביז אהין. דערנאך נעם איך אוועק יעצט יעדעס דריטע נומער אינעם סיִקווענס און איך טויש יעדעס נומער אין דעם סיִקווענס לויט די סומע פון אלע נומערן וואס קומען בעפאר ביז אהין. דערנאך נעם איך אוועק יעדעס צווייטע נומער אינעם סיִקווענס און איך טויש יעדעס נומער אין דעם סיִקווענס לויט די סומע פון אלע נומערן וואס קומען בעפאר ביז אהין. דאס גייט מיר געבן:
1⁴,2⁴,3⁴,4⁴…

אויב נעם איך ארויס צום ערשט יעדעס טרייענגולער נומער און איך רעכן אלע נומערן ביז אהין פון וואס בלייבט איבער און איך טויש עס מיט דעם, באקום איך די סיִקווענס פון די פעקטאָריעלס:
1!,2!,3!,4!…

אז מ׳האט אויבן גערעדט אין די געדאנק פון דאָבּל-נעגעישאן לגבי מגדיר זיין ״ג-ט״, איז כידוע דא צוויי סארטן דראָגס: אינהיבּטארי, וואס האלטן צוריק ניוראָטראסמיטארס אינעם מח, און עקסייטעטארי, וואס טוהן דאס פארקערטע. אלקאהאל איז אַן אינהיבּיטארי דראָג וואס (ווי דר. פּאָל בּלום איז דאס מסביר אין די לעקציע [27:06-27:15]) טוהט אינהיבּיטן די אינהיבּיטאָרי חלקים פונעם מח (הגם באמת זענען די חלקים אין ראם פון עקסייטעטארי) וואס האלטן אין אלגעמיין צוריק דעם מענטש, ולכן איז א שיכור ווילדער וכדומה.

ולפי״ז טרעפט מען אזא סארט ענליכן געדאנק פון א דאָבּל-נעגאטיוו ביי יין. האב איך געקלערט אז מ׳קען מיט דעם זאגן א רמז בהגמרא בעירובין סה. א״ר חנינא כל המתפתה ביינו יש בו מדעת קונו ע״ש. והיינו, אז ער פארשטייט די געדאנק פונעם דאָבּל-נעגאטיוו שבהיין, וואס די געדאנק איז לגבי לדעת את קונו וככל הנ״ל. (און דאס קען אויך זיין די רמז דארט פון נכנס יין יצא סוד. און דאס קען אויך זיין די געדאנק פון, סנהדרין ע., חמרא וריחני פקחין.)

ובכל זה, דער אסטראנאמער דזשעימס דזשיִנס האט געזאגט, "ג-ט איז א מאטעמאטיקער". און ווי דזשים האָלט שרייבט לגבי די חקירה אינעם פילאזאפיע פון מאטעמאטיקס צי מאטעמאטישע מושגים טוהן "עקזיסטירן" ממש טאקע (אין אן אנטאלאגישן זין): און פונקט אזוי ווי דארט ביי מאטעמאטיקס פארשטייט מען אז די תירוץ צום לעצטן שאלה זיינער איז ל"ד "יא", איז ביי טעאלאגיע אויך, וואו די דריטע עיקר קומט אזוי כעין נעגעיטן דעם ערשטן עיקר וככל הנ"ל, אויך די תירוץ צו די שאלה דערביי ל"ד "יא".

***

ווען לייבניץ האט געוואלט מסביר זיין פאר די מלכה סאָפיִאַ טשאַרלאט פון Prussia די געדאנק פון אינפיניטלי קליין [אינפינטעסימעל], האט זי געזאגט אז עס פעהלט נישט אויס ווייל זי ווייסט דאס זעהענדיג אירע יועצים...

אז מ׳האט גערעדט פון מעיטריסיִס ובענין סיִקווענסעס איז אינטרעסאנט צוצוצייכענען צום נומער וואנט. דאס איז וואו איך שטעל אויס א שורה פון 1׳ס איינס נאכ׳ן צווייטן. גראד אונטער דעם שטעל איך נאכדעם א שורה פון עני נומערן איך וועהל אויס. דערנאך שטעל איך אויס דערין נומערן אזוי אז יעדעס נומער זאל זיין די סקווער פון די סומע פון די פראדוקט פון די נומערן צו אירע רעכטע און לינקע זייט און די פראדוקט פון די נומערן העכער איר און אונטער איר. מיינענדיג, אז ווען איך מאָלטיפּליי די נומער וואס איז גראד צו רעכטס פונעם נומער צוזאמען מיט די נומער גראד צו לינקס פונעם נומער, און איך לייג צו צו דעם די פראדוקט ווען איך מאָלטיפּליי די נומער גראד העכער דעם נומער מיט די נומער גראד אונטער דעם נומער, און דערנאך סקווער איך עס [איך מאָלטיפּליי עס ביי זיך אליין] וועט עס זיין אט די נומער אינדערמיט. (ווען איך שטעל אויס דעם וואנט ווייטער ווייס איך בדרך כלל וואס איז שוין די מיטעלסטע נומער און איך דארף געוואור ווערן, דורך אלדזשעברא, וועלכעס איז א נומער וואס פעהלט ארום איר.)

‏(עס איז אביסל ענליך צו פּאַסקאַל׳ס טרייענגעל.)

א נומער וואנט העלפט מיט׳ן קענען דעצידירן וואס קומט דערנאך אין א סיִקווענס וואס מ׳געבט דיר. והיינו, איך שטעל אט די סיִקווענס אונטער די שורה פון 1׳ס. ביי א געוואלד סיִקווענסעס וואס גייען מיט עפעס א סדר וועט די נומער וואנט זיך עווענטועל ענדיגן מיט נאר שורות פון 0,ס. למשל, דא ביי די סיִקווענס פון סקווערס: דאס האלט אויך אָן ביי די סיִקווענס פון קיוּבּס, העכערע פּאַוּערס/עקספּאָנענטס, ואפילו די פיבּאָנאַטשי סיִקווענס.

איז אויב זעה איך אז דאס פאסירט מיט די נומער וואנט פון דעם סיִקווענס, דאן וואס איך טוה איז אז איך שטעל אויס די נומער וואנט מיט די סיִקווענס און טויש די צווייטע שורה, וואס איז די געגעבענע סיקווענס, צו די נומער מיינוס די נומער וואס קומט פאר דעם אינעם סיִקווענס טיימס x. דערנאך שטעל איך אויס ווייטער די נומער וואנט עפ״י די הלכות הנ״ל נאר מיט די הלכות ווען איך מאָלטיפּליי א וועריעבּל. ביים שורה העכער וואו דח שורה דארונטער זענען 0׳ס, קומען זיי אויס צו בעצם די זעלבע פּאַלינאָמיעל און ווען איך סאַלוו דאס און טערמינען פונעם העכסטן דעגרי [די נאָמיעל וואס האט דאס גרעסטע עקספּאָנענט] איז דאס רעכען איך אלס די מקום וואס איך וויל אָנפילען אינעם סיִקווענס, די צווייט העכסטע נאָמיעל איז די פלאץ אינעם סיִקווענס פאר דעם, די דריט העכסטע איז צוויי פלעצער אינעם סיִקווענס פאר דעם, אא״וו. ווען איך פאלג די עקוועישאן געבט דאס מיר דעם נומער איך זוך.

עס איז אינטרעסאנט צו באמערקן אז די פּאַלינאָמיעל איך באקום פונעם נומער וואנט וואס איך מאך פאר׳ן פיבּאָנאַטשי סיִקווענס: און אז איך סאַלוו דאס באקום איך: וואס דאס איז די גאלדענע רעישיאו וואס איז מקושר צום פיבּאָנאַטשי סיִקווענס.

עס קומט אויך אויס אז יעדעס מאל עס איז דא א 0 אין א נומער וואנט גייט עס אדער זיין אליינס אדער שאפן א פונקטליכע סקווער: 4 0׳ס צוזאמען, 9 0׳ס צוזאמען, 16 0׳ס צוזאמען אא״וו. און ווען עס איז דא איין 0 ארום א נומער אינעם וואנט קעגנאיבער דעם נומער וואס איך וויל געוואור ווערן קען עס מאכן א פראבלעם וויבאלד 0 טיימס די וועריעבּל וואס איך וויל וויסן וועט עס אטאמאטיש מבטל זיין. דאן איז וואס איך טוה איז כזה: איך עקסטענד דאס און איך סקווער אלע נומערן וואס זענען הארט נעבן דעם נומער אינעם וואנט. דערנאך מאָלטיפּליי איך די אין די שתי וואס זענען נעבן מיט די אויף די אנדערע זייט קעגן זיי אינעם שתי וואס זענען מער אינדרויסן [פונעם זעלבן קאליר אינעם בילד] און איך טוה דאס נאכאמאל פארקערט אבער ווייטער אינעם שתי, און דאס דארף אויסקומען די זעלבע ווען איך טוה די זעלבע שפיל אינעם ערב. עס זענען דא אנדערע לומדות׳ן צו טוהן ווען די סקווערס פון די 0׳ס זענען נאך גרעסער כנ״ל.

בנוגע די קשר צווישן מאטעמאטיקס און אמונה וואס מ׳האט גערעדט אינעם אשכול איז אינטרעסאנט צוצוצייכענען צו וואס דער פראנצויזישער מאטעמאטיקער זשאַן לע ראַנד ד׳אַלעמבּערט האט געזאגט לגבי רעכענען אינפיניטעסימעלס, די אינפיניטלי קליין: ״גיי ווייטער, און די אמונה [אין זייער עקזיסטענץ] וועט שוין קומען צו דיר.״

ועוד בזה (מיט הומאר): ***

ולגבי גאָדעל׳ס טעארעם האט דער פיזיקער דזשאַן אַרטשיבּאָלד וויִלער געקלערט אז עס איז מעגליך דא א קשר צווישן דעם טעארעם און הייזענבערג’ס אָנסירטענטי פּרינציפּ אין קוואנטום פיזיקס. ער איז געגאנגען דאס פרעגן פון גאָדעל אליינס. גאָדעל איז געווארן ברוגז און אים ארויסגעווארפן פון זיין אפיס.

בנוגע גאָדעל׳ס טעארעם איז דא אין קאמפּיוטער סייענס/מאטעמאטיקס די געדאנק פון קאָלמאָגאָראָוו קאמפּלעקסיטי. דאס איז די מעסטונג פאר א געוויסע זאך די מינימום/קערצסטע פראגראם (אין א געוויסע פראגראמינג שפראך), אין אינפארמאציע/בּיטס, וואס געבט ארויס אט די זאך (מיט איר אינפארמאציע) ווען די פראגראם לויפט אויף אַן איידיעלייזד קאמפיוטער מיט אָנלימיטעד מעמארי. אין אנדערע ווערטער, עס איז א מעסטונג פון א זאך אין די קלענסטע וועג איך קען ענקוֺידן איר אינפארמאציע אין בּיינערי. (דאס האט א שייכות מיט סאלאמאנאף׳ס טעאריע פון יוניווערסאל אינדאקטיוו אינפערענס.)

אין דעם איז דא טשעיטין׳ס אינקאָמפּליִטנעס טעארעם. דאס לויטעט אז עס איז אלס דא א נומער וואס מ׳קען נישט אויפווייזן אז די קאָלמאָגאָראָוו קאמפּלעקסיטי פון עני ספּעציפישע סיִקווענס פון אינפארמאציע/בּיטס (וואס יעדעס זאך איז דאך בעצם אינפארמאציע און קען ווערן ענקוֺידעד אלס א סיִקווענס פון בּיטס/אינפארמאציע) איז מער ווי דעם. דאס מיינט אז פאר יעדעס נומער איז דא אַן אינפיניט צאל סיִקווענס פון אינפארמאציע/בּיטס וואס האט א קאָלמאָגאָראָוו קאמפּלעקסיטי מער ווי דעם (ווייל עס איז דאך דא א גבול פון וויפיל קורצע פראגראמען עס זענען פארהאן), אבער מ׳קען נישט ווייזן אויף א געוויסע ספּעציפישע סיִקווענס פון אינפארמאציע/בּיטס און אויפווייזן אז איר קאָלמאָגאָראָוו קאמפּלעקסיטי איז מער ווי דעם.

די נומער ווענדט זיך אין די פראגראמינג שפראך מ׳נוצט און די סיסטעם פון מאטעמאטיקס מ׳נוצט. (אַן upper bound דערויף איז ממש אפאר קילאבּייטס.)

‏דאס קען ווייטער האבן א שייכות מיט די טעאלאגישע שמועסן אין דעם אשכול, לגבי דעם ווי ריבוי וקאמפּלעקסיטי קומט פון פשטות. ועיין לדוגמא בעיקרים מאמר ב פי״א.


ועיין כאן.

***

ולגבי די געדאנק פון עוסק זיין אין pure חכמה און די נוצליכקייט דערפון, פארציילט מען אז דער בריטישער פינאנץ מיניסטער איז אמאל געקומען באזוכן מיכאל פאראדעי. זעה׳ענדיג עקספּערימענטן אין עלעקטראָמאַגנעטיזם האט ער געפרעגט, ״וואסערע נוצן איז דא דערפון?״ האט אים פארטדעי גע׳ענטפערט, ״איך ווייס נישט. אבער איין טאג וועסטו נאך בעהטן דערפון שטייערן.״

***

דער מאטעמאטיקער דר. מעלווין נעטענזאן דערציילט: ער דערציילט סתם אזוי: ער ברענגט ארויס אז אויפקומען מיט חידושים במאטעמאטיקס ארבעט בעסער ווען מ'ארבעט אליין ווי איידער בחברותא. גייט דאס שוין ווייטער צוזאמען מיט טעאלאגיע אין דעם געביט אז פשטות איז בעסער ווי ריבוי.

ווי געזאגט איז ווען מען געבט אַן עקספּאָנענט פון 4, אדער א מאָלטיפּל דערפון [עני נומער איך קען דיוויידן ביי 4 אָן א רימעינדאר] צו i ברענגט עס דאס צוריק צו א געהעריגע פאזיטיווע 1. דאס באדייט אז i ווערט גערופן די רוּט פון יוּניטי פאר 4 און אירע מאָלטיפּלס. דאס איז ווייל א רוּט פון יוּניטי איז ווען איך וועהל א נומער אלס אַן עקספּאָנענט, און פאר א ספּעציפישע בּעיס (אימעדזשינערי/קאַמפּלעקס) נומער וועט מיר די עקספּאָנענט דאס ברענגען צו 1, דאן איז די בּעיס דאס רוּט פון יוּניטי פאר די בּעיס נומער. טאמער איז נישטא קיין קלענערע עקספּאָנענט איך קען וועהלן דערפון פאר די בּעיס און אזוי עס מאכן צו 1, דאן איז דאס די פּרימיטיוו רוּט פון יוּניטי פון די בּעיס. עס קומט אויס אטאמאטיש אז אויב איז די עקספּאָנענט א פּריים דאן איז דאך דאס בהכרח די פּרימיטיוו רוּט פון יוּניטי פון די בּעיס - עס איז דאך נישטא קיין קלענערע מאָלטיפּל דערפון.

אין דעם איז דא די סיריִס וואס רופט זיך די גאַוּס קראַדוועטיק סומע. דאס איז וואו איך וועהל איין פּריים און איין אינטעדזשער. איך הייב דערנאך אָן פון 0 ביז איינס ווייניגער ווי א די פּריים איך האב אויסגעוועהלט. און ביי יעדעס נומער פון 0 ביז אהין נעם איך די סקווער פון דעם נומער וואו איך האלט און איך מאָלטיפּליי דאס ביי די אינטעדזשער איך האב געוועהלט. און וואס איך באקום געב איך אלס אַן עקספּאָנענט צום (בּעיס) נומער וואס איז די (פּרימיטיוו) רוּט פון יוּניטי פון די פּריים נומער איך האב געוועהלט. דאס טוה איך ביי יעדעס נומער פון 0 ביז איינס ווייניגער פונעם פּריים איך האב געוועהלט. דערנאך עדד איך אלעס וואס איך באקום צאם. איך קען וויסן וואס איז די רוּט פון יוּניטי פאר׳ן פּריים דורך דאָפּלען פּיי/דאס וואס די היקף פון א סירקעל איז מער ווי איר רוחב [π], דאס מאָלטיפּלייען ביי i, און דאס דיוויידען ביים פּריים. דערנאך געב איך דאס וואס איך באקום אלס אַן ערספּאָנענט צו אוילער׳ס נומער פון 2.718… (דאס האט א שייכות מיט אוילער׳ס אידענטיטעט וואס @שליח האט דערמאנט.)

דער מאטעמאטיקער דר. שמואל פּעטערסאן האט אויפגעוואוזן, מיוסד אויף טאמער די ריעמאן היפאטעזיע איז אמת, אז טאמער אנשטאטס סקווערן דעם נומער וואו איך האלט ביי אינעם פריערדיגן פּראצעדור, טוה איך קיוּבּן די נומער, דאן ווען איך רעכען צאם א צאל גאַוּס קראַדוועטיק/קיוּבּיק סומעס גייען זייערע סומעס צוזאמען זיין בערך אט די צאל פון גאַוּס קראַדוועטיק/קיוּבּיק סומעס געהעכערט צו אַן עקספּאָנענט פון 5 און דערנאך גענומען דעם זעקסטן רוּט דערפון [וועלכע נומער מאל וועלכע נומער וכו׳ 6 מאל, וועט מיר ברענגען צו דעם נומער].