אלזא, דער ענטפער אין קורצן איז, (אזוי ווי איך האב מרמז געווען ביים קעפל ״איז דאס א טרייענגל ??? ), אז די אויג ווערט דא גענארט, און עס איז נישט קיין דריי-עקיגע פארם, נאר א פיהר-עקיגע פארעם. (אזוי ווי [tag]געפילטע פיש[/tag] האט גע׳טענה׳ט).
אבער וואס, און ווי אזוי, פעלט זיך אויס א שטיקל אריכות, און קודם צוויי הקדמות.
1. יעדע ענגל (ווינקל) קען ווערן געמאסטן אין דיגריס, כידוע. די שיפע ליין (אדער ״אלכסון״) פון א רעכט-טריי-ענגל (ד. ה. א טריי ענגל וואס איינס פון די ענגלס זענען 90 דיגריס), קען ווערן געמאסטן זייער גרינג, ווי פאלגענד:
מען נעמט די הויכקייט פונעם טרייענגל און מ׳צוטיילט איהם אין די לענג פונעם טרייענגל (ווען די הויכקייט איז קלענער פון די לענג), באקומט מען עפעס א נומער, און מען לייגט עס אריין אין א סייענטיפיק קאלקעלעיטער (scientific calculator), און מען דריקט inverse, אין דערנאך דריקט מען sin, (נאכן מאכן זיכער אז די קאלקעלעיטער איז אנגעשטעלט אויף deg, און נישט אויף rad), (מעגליך אז ס׳וועט ארויפקומען נאכן דריקן inv, א קליינע מיינוס 1 אויף די רעכטע זייט פון דאס ווארט sin), באקומט מען די נומער פון דיגריס, ווי שיף דער אלכסון איז (אדער וויפיל איז די ענגל וואס איז צווישן איהם און די לענג).
עס איז נישט אזוי וויכטיג צו פארשטיין ווי אזוי מען רעכענט עס, דער עיקר איז אז עס איז קלאר אז יעדע רעכט-טריי-ענגל קען ווערן גערעכנט פונקטליך, צו וויסן ווי שיף זיין אלכסון איז.
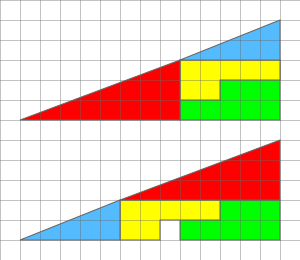
2. ווען עס זענען דא צוויי טרייענגלס וואס זענען דומה (״דומה״ איז נישט ״גלייך״), דאס הייסט אז אלע דריי ווינקלען פון די צוויי טרייענגלס זענען די זעלבע דיגריס ביי ביידע טרייענגלס, (ווי למשל 90,40,50), כאטש וואס די לענג פון זייערע זייטן זענען נישט די זעלבע גרויס. דעמאלטס קען מען מאכן פון די צוויי א דריטע גרויסע טרייענגל, (אזוי ווי עס זעהט לכאורה אויס אין אונזער בילד, די בלויע און די רויטע פארעמען א נייע טרייענגל), וואס די נייע טרייענגל, איז אויך דומה צו די צוויי קליינע.
ווי למשל האבנדיג א טרייענגל וואס זיינע זייטן זענען 3,4,5. און נאך א טרייענגל וואס זיינע זייטן זענען 6,8,10. אז מ׳גייט אויסרעכענען וועט מען זעהן אז די אלכסון ביי ביידע איז די אלכסון שיף 48.59 דיגריס. אזוי אויך אויב מ׳וועט מאכן פון זיי צוויי א דריטע גרויסע טרייענגל, וועט זיין די לענג פון די זייטן 9,12,15, און דער אלכסון ביי אלע דריי איז די זעלבע (3/4).
יעצט בנידון דידן, אז מיר וועלן אויסרעכענען דעם קליין בלויע טרייענגל וועט מען באקומען 2/5 וואס איז אינעם דעצימל שפראך 0.4 וואס קומט אויס 23.57 דיגריס בערך. ווידער די רויטע טרייענגל איז 3/8 וואס איז 0.375, וואס קומט אויס צו זיין בערך 22.02 דיגריס.
סא, זעהן מיר קלאר אז די צוויי קליינע טרייענגלס זענען ״נישט״ דומה, דאס הייסט די אלכסון פונעם בלויע טרייענגל איז אביסל מער ארויף ווי דעם רויטן, (נאר ס׳איז גענוג א קליין חילוק אז דער אויג זאל עס נישט באמערקן), איז ממילא קומט אויס אז די גרויסע אזוי גערופענע טרייענגל, איז בכלל נישט קיין דריי עקיגע פארעם, נאר א פיהר עקיגע פארעם.
און אנדערע ווערטער, ביים אויבערשטן צאמשטעל, איז עס אריין געשטעקטע ווינקל, און ביים אונטערשטן צאמשטעל איז ער ארויס געשטעקט.
(וואלט ער געווען אן אמת׳ע טרייענגל, וואלט זיין שטח געווען גרויס 5*13/2 וואס איז 23.5, אבער למעשה בנידון דידן, איז די אויבערשטע פארעם גרויס 7+8+10/2+/24/2=32, און דעם אונטערשטן איז 32+1=33. אזוי ווי [tag]געפילטע פיש[/tag] האט גערעכנט.
דאס ווייזט אונז אז דער אריין געשטעקטקייט פונעם אויבערשטן האט געמאכט דערלייגן א האלבע קעסטל, און די ארויס געשטעקטקייט פונעם אונטערשטן האט געמאכט פארדינען נאך א האלבע קעסטל.
און טאקע אויב איהר וועט רעכענען די גרויס פון די אומזעהבארע טרייענגל וואס ווערט געפארעמט פון די אריין געשטעקטקייט און ארויס געשטעקטקייט, דאן וועט איהר זעהן אז ער איז גרויס פונקט האלב, ווי איך וועל רעכענען אין א עקסטרע הודעה).
כדי צו קלאר מאכן פאר די וועלכע כאפן נאכנישט, וועל איך ברענגען א בילד פון אביסל אן אנדער מעשה, וואס דער חילוק צווישן די צוויי טרייענגלס זענען היבש גרעסער, און איהר וועט אליינס זעהן דעם געדאנק.
אט דא קען מען זעהן, די בלויע איז 3/5 (0.6) און די רויטע איז 3/9 וואס איז (0.333), דאן די דיגריס ביי די בלויע איז 36.86, און ביי די רויטע 19.47), דעמאלטס כאפט שוין די אויג גלייך דעם חילוק, און אלעס איז קלאר.…
די בילדער זענען גענומען געווארן פונעם וואונדערליכן בלאג ״לא מדויק״ פון גדי אלכסנדרוביץ, מיט זיין ברייט הארציגע רשות.
http://www.gadial.net/2007/10/24/triangle_illusion/