קאווע שטיבל

[center]חלק א[/center]

עס איז די וואך געווארן באריכטעט אין די צייטונגען איבער א 15-יעריגער אינגל, וועלכער איז געפארן אויף א פאמיליע-אויספלוג קיין באסטאן, א שטאט וואו זיי גייען אפט באזוכן, ער איז געגאנגען צוזאמען מיט זיינע פעטערס באזוכן די סייענס-מוזיעם אין באסטאן, און האט אויפגעכאפט א טעות אין די מאטאמטיק-אפטיילונג. דער 15 יעריגער יוסף ראזענפעלד האט באמערקט אז די עקוועיזשן וואס עס שטייט פאר די גאלדען-רילעישן איז נישט ריכטיג, (אנשטאט א מיינוס דארף שטיין א פלוס).

אין אנפאנג, איז ער געווען אומ-זיכער, ער האט געטראכט קען זיין אז עס זיין טעות, אבער ער איז געווען איבערראשט – דערציילט ער. נאך אלעם רעדט מען דא פון א פארשטעלונג וואס איז געשאפן געווארן דורך געלערנטע לייט, און עס שטייט שוין זינט 1981, אבער ער האט איבערגעקוקט אין וויקיפידיע, און ער האט געזעהן אז ער איז גערעכט. ער האט איבערגעלאזט א מעסעדזש ביי די פראנט-דעסק, אהן איבערגעבן זיין קאנטאקט-אינפארמאציע, און ממשיך געווען אין זיין וועג.

שפעטער, ווען יוסף'ס פעטער האט ווידער געקאנטאקט די מוזיעם, האבן זיי איהם צוריק געשריבן א בריוו: "איהר זענט גערעכט אז די פורמאלא פאר די גאלדען-רילעישן איז נישט ריכטיג, מיר וועלן עס איבער טוישן אין די דריי פלעצער וואס זיי געפונען זיך, (אנשטאט די – סיין, וועלן מיר שרייבן די + סיין). אויב מיר וועלן נישט דארפן טוישן די ארגינעלע".

נאך 35 יאהר וואס די מוזיאום האט דאס געהאט אין זייער פארשטעלונג, האט א פופצן יעריגער בחור'ל זיי אויפמערקזאם געמאכט איבער זייער אפענע גרייז. און דערמיט זוכה געווען צו ווארעמע העד-ליינס.
שוין, א שיינע מעשה. אהה.. כ'האב שיעור פארגעסן, אין י-נעט זאגן זיי אז דער בחור איז גאר א יוד. נו, פארשטייט זיך, ממש ערווארטעט.

עד כאן המעשה.
אבער דער אמת איז, אז לא דובים ולא יער, עס פאנגט זיך נישט אן די גאנצע טעות, און די עקוועיזשן וואס איז געשטאנען דארטן איז נישט געווען קיין טעות. נאר וואס דען? לאמיר קודם אביסל עקספלארן אט דעם קאנסעפט, און לאמיר פראבירן פארשטיין וואס דאס מיינט:

וואס איז עס?

דער גאלדען רעשיאו טוהט שוין באשעפטיגן ארטיסטן צוזאמען מיט מאטעמאטיקער פאר הונדערטער יאהרן, די היסטאריע גייט שוין צוריק צו דעם גריכישן "פיטאגאראס", און אזוי אוקלידוס ברענגט עס אויך אין זיין ספר "יסודות".

קודם אין קורצן, די גאלדען רעישיו איז א מאטעמאטישע קאנסטענט [1] וואס טוהט רעפרעזענטירן דער נומער וואס אויב מ׳נעמט אראפ פון איהם איינס, און מיר באקומען עפעס א רעזולטאט, און דערנאך צוטיילט מען איינס אין די רעזולטאט, באקומט מען צוריק דעם נומער.

אביסל קלארער און צושטאטעלעך: מיר זוכן אזא סארט נומער (לאמיר איהם רופן A), וואס אויב נעמען מיר אראפ פון איהם דעם נומער 1, (וועלן מיר באקומען A-1), און דערנאך וועלן מיר מאכן 1 צוטיילן אין A-1, זאלן מיר צוריק באקומען A.

למשל, לאמיר טרייען A זאל זיין 1.8, ווען מיר נעמען אראפ פון איהם 1 באקומען מיר 0.8, יעצט אויב טוהן מיר : 1 צוטיילן אין 0.8, באקומען מיר 1.25. דאס איז נישט A. אויב אזוי איז 1.8 נישט די ריכטיגע ענטפער.

אין סימבאלס:
[center]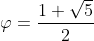[/center]

און אין דידזשיטס:
[center]...1.6180339887498948482045868343656[/center]

די דריי נומערן ביים סוף רעפרעזענטירן ענדלעס נומערן, מיינענדיג דערביי צו זאגן, אז עס איז ממשיך ווייטער עד אין סוף (כפשוטו).

אבער פאר אונז פשוט'ע חסידישע יונגעלייט, מיר ווייסן נישט פון קיין איקסעס און עקוועיזשן צו זאגן, אבער בוכאשעם א קאלקולעיטער האבן מיר, און עטליכע פון אונז האבן אויך ענערגיע און רצון צו פראבירן טרעפן אט דעם נומער, אלזא, לאמיר פשוט זיך ארויסלאזן אויף א זוכעריי צו איהם טרעפן.

פאנגען מיר אהן אזוי, לאמיר זאגן אז ער איז 1.5, טעסט: 1.5 מיינוס 1 איז 0.5, אויב וועלן מיר מאכן 1/0.5 וועלן מיר באקומען 2.

אויב אזוי איז 1.5 צו קליין, וועלן מיר נעמען 1.6, טעסט: 1.6 מיינוס 1 איז 0.6, 1/0.6 איז 1.6666, אהה.. אביסל נענטער (עס הייסט - 1.6 איז נאנט צו .....1.666), אבער נאך אלס צו קליין.

דאן לאמיר נעמען 1.7, טעסט: 1/0.7 איז 1.42 מיט סענטס, אויב אזוי איז עס שוין צו גרויס.

דאן לאמיר פראבירן 1.65, טעסט: 1.53 ווידער צו גרויס.

דאן לאמיר פראבירן 1.63, טעסט: 1.58, צו גרויס.

און אזוי ווייטער.... עס וועט אייך נעמען גאנץ לאנג, אבער עס איז אזוי פיהל פארזיכערט, אז אויב טוהט איהר עס ריכטיג וועט איהר קומען נענטער און נענטער צום ריכטיגן ענטפער. (אקעי, באקומען פונקטליך די ריכטיגע ענטפער וועט איהר קיינמאל נישט, אויך נישט מיט קיין קאלקולעיטער).

------

פאר די וועלכע ווילן די אלג'עברישע צוגאנג דערצו, וועל איך עס רעפרעזענטירן:
כדי צו באקומען די נומער, דארפן מיר פשוט פרעגן די פראגע וואס ווילן מיר האבן? איז אזוי מיר ווילן עפעס א נומער (לאמיר איהם רופן x, כנהוג), וואס אויב נעמען מיר אראפ פון איהם 1, און מיר צוטיילן איינס אין איהם באקומען מיר איינס, לאמיר עס אביסל מאטעמאטיש סימבאליזירן:



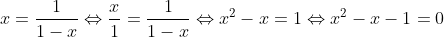
איינמאל מיר האבן דא א סטאנדארט קוואדראטיק עקוועיזדשן, וועל איך איינלאדענען אונזער אלעמען באקאנטן [tag]יידל[/tag], צו סאלוון די עקוועיזדשן.


מער פרטים אינעם קומענדיגן/ע ארטיקל/ען.

[1]. א מאטעמאטישע קאנסטענט (אזוי ווי: פיי, אי, איי, און נאך), אנדערש ווי א וועריעיבל, וואס רעפרעזענטירט א סימבאל פאר א טוישבארע נומער, מיינענדיג דערמיט אז מ'רעדט נישט פאר א ספעציעלע נומער, א קאנסטענט איז אבער א סימבאל וואס ווערט גענוצט אייביג פאר די זעלבע נומער, געווענליך א נומער וואס האט א ספעציעלע מאטעמטישע באדייט.

שכח הרב @פארוואס פארן אונז כסדר געבן אן אריינבליק אינעם גרויסן פעלד פון מאטעמאטיקס אולי וועלן מיר נאך זוכה זיין אמאל עס צו פארשטיין אויך,

למעשה איז דא אזא נומבער אדער איז עס בלויז א שפיל צו ווייזען אז עס איז נישטא אזא נומבער?

הננו מוכן ומזומן לקיים מצות ועשית ככל אשר יוריך ליקב"ו בדחילו ורחימו ליחד שם י"ה בו"ה.

מיר שמועסן דאך דא אז די פיינעל איקוועזשאן וויאזוי צו רעפרעזענטירן דעם נומער, איז:

[center][/center]

וויאזוי ווייסן מיר וואס X איז (דהיינו אז אויב טוישן מיר אויף X מיט דעם נומער וועט די איקוועזשאן שטימען)?

מיר נוצן די קוואדרעטיק פארמולע. די קוואדרעטיק פארמולע איז אן אור-אלטע פארמולע וואס אן אראבישער מאטעמאטיקער האט אויסגעארבעט גענוי פאר דעם פראבלעם. דער פארמולע זעט אויס אזוי:

[center][/center]

a איז די נומער (coefficient) בעפאר דעם ערשטן טייל (x^2), אין אונזער פאל איז דאס א פשוט'ער 1.
b איז די נומער (coefficient) בעפאר דעם צווייטן טייל (x), אין אונזער פאל א נעגאטיוו 1.
און c איז די לעצטע טייל, אין אונזער פאל אויך א נעגאטיוו 1.

אז מיר וועלן דאס אריינשטעלן אין אונזער פארמולע, און אויסטוישן a, b, און c מיט די ריכטיגע נומערן, באקומען מיר דאס:

[center][/center]

מיר דארפן דאס אביסל סימפליפייען צו אנקומען צום ענדגילטיגן רעזולטאט. לאמיר גיין לינקס צו רעכטס.
נעגאטיוו נעגאטיוו 1 איז פאזעטיוו 1.

נעגאטיוו 1 סקווערד איז 1

4 טיימס 1 טיימס נעגאטיוו 1 איז נעגאטיוו 4.

אז מיר רעכענען צוזאם די צוויי נומערן אינעם דיסקרימינענט (discriminant - דאס איז די חלק אונטערן סקווער רוט סימבאל אינעם קוואדרעטיק פארמולע) האבן מיר 1 מיינוס נעגאטיוו 4 וואס איז איקוואל 5:

אינעם דינאמינעטאר (denominator - די חלק אונטערן פרעקשאן ליין) האבן מיר 2 טיימס 1 וואס איז איקוואלס צו 2.


די פיינעל רעזאלט איז

[center][/center]

און וויבאלד X איז פאזעטיוו, רעדן מיר דאך דא פון א רעשיא וועלכע א פאזעטיוו, און דעריבער איז די פיינעל רעזאלט:

[center][/center]


דאס קומט אויס בערך:
1.6180339887498948482045868343656381177203091798057628621354486227052604628189024497072072041893911374847540

גראדעמעכעלע האט געשריבן:שכח הרב @פארוואס פארן אונז כסדר געבן אן אריינבליק אינעם גרויסן פעלד פון מאטעמאטיקס אולי וועלן מיר נאך זוכה זיין אמאל עס צו פארשטיין אויך,

למעשה איז דא אזא נומבער אדער איז עס בלויז א שפיל צו ווייזען אז עס איז נישטא אזא נומבער?

יא. עס איז פארהאן אזא נומער, אזוי איך וועל מאריך זיין אינעם קומענדיגן ארטיקל.

אבער עס איז אנדערש ווי די גאנצע נומערן וואס מער קענען, (אזוי ווי 1, 2, 3, און ווייטער).
און ניטאמאל קיין ראציאנאלע נומער. (אזוי ווי א האלבע, א דריטל, און אזוי ווייטער).

א גרויסן יישר כח, יידל און פארוואס, פאר דעם שמועס. איך האב קיינמאל נישט דורכגעטון די נושא פון די גאלדענע ראציאן און לויט ווי איך הער זעט מען גרויסע נפלאות הבורא דערין. וועלן מיר ווארטן מיט שפאנונג.

פארוואס? האט געשריבן:

גראדעמעכעלע האט געשריבן:שכח הרב @פארוואס פארן אונז כסדר געבן אן אריינבליק אינעם גרויסן פעלד פון מאטעמאטיקס אולי וועלן מיר נאך זוכה זיין אמאל עס צו פארשטיין אויך,

למעשה איז דא אזא נומבער אדער איז עס בלויז א שפיל צו ווייזען אז עס איז נישטא אזא נומבער?

יא. עס איז פארהאן אזא נומער, אזוי איך וועל מאריך זיין אינעם קומענדיגן ארטיקל.

אבער עס איז אנדערש ווי די גאנצע נומערן וואס מער קענען, (אזוי ווי 1, 2, 3, און ווייטער).
און ניטאמאל קיין ראציאנאלע נומער. (אזוי ווי א האלבע, א דריטל, און אזוי ווייטער).

פאר א הערליכע הסברה איבער די באדייט פון ראציאנעלע און אומראציאנעלע נומער זעט דא אין די לענגערע תגובות פון החכם הכולל @יידל.

איך וועל פראבירן ברענגען איין דוגמא, וואו מ׳שטויסט זיך אן אין דעם אין ריעל לייף שפעטער.

שכויח פאר די לינק, כ׳האב געהאט בדעה עס צו לינקען אין די קומענדיגע ארטיקלען.

(און בדרך אגב, זעה איך אז דו האסט געטייטשט ratio צו ראציאן, איז עס אן אייגן געמאכטע ווארט?).

[center]חלק ב[/center]

איך האב שוין איין מאל גערעדט פון אן אי-רעישנאל נומער, איך וועל קודם אביסל פארברייטערן איבער אי-רעישנל נומערן אין אלגעמיין, און דערנאך וועל איך זיך בעיקר קאנצעטרירן אין אונזער.

כדי צו פארמיידן פילאסאפישע וואסער געמאלענע טענה׳רייען, וועל איך קלאר שטעלן וואס איך מיין צו פרעגן צו עס עקזיסטירט א נומער. לאמיר זיך פארשטעלן אלע נומערן ווערן אויסגעלייגט אין א ליניע, צווישן יעדע נומער איז געצויגן א ליניע אין אן אייניגע מאס, (אזוי ווי א רולער). עס איז איין גלייכע לאנגע ליין אהן קיין שום לאך אינצווישן. קענען מיר ערגעצוואו אויפן ליין אנדייטן אויף א פינטל אין דעם ליין, אז דארטן איז אונזער נומער?

(פאר א מער דעטאלירטע ערקלערונג, קענט איהר לייענען די וואונדערבארע אשכול מעשי ידיו פון [tag]יאיר[/tag], מיטן קעפל "בואו חשבון").

אויב וועט איהר פרעגן פאר איינעם וואס האט אביסל געלערנט ליניער-אלגעברא, וועט ער אייך ענטפערן אז אזא נומער איז פארהאן, און אז אזעלכע נומערן זענען דא אן א שיעור [1].

היינטיגע צייטן מיט מאדערנערע אלגעברא זאגט זיך אז אזא נומער עקזיסטירט פשוט מיטן סאלוון דעם איקס פאר די עקוועיזשן: , באקומען מיר צוויי סאלושענס (א נעגעטיווע און א פאזיטיווע), די פאזאטיווע סאלושן, דאס איז אונזער נומער וואס מיר דארפן.[2].

אבער צוריק-גייענדיג אין די היסטאריע, ווען מאטעמאטיק (און סייענס בכלל) איז נאך געווען אין איהרע ווינדלען, איז עס נישט געווען אזוי פשוט, אין פאקט, פאר זייער א לאנגע תקופה האבן די גריכישע געלערנטע געהאלטן אז עס איז נישט פארהאן קיין אומ-ראציאנאלע נומערן, אויף אזוי ווייט אז עס איז דא א לעגאנדע אז איינע פון די פיטאגאריסטן וועלכע האבן אויסגעפונען אן אומ-ראציאנלע נומער, האבן זיי איהם דערטרונקען אין די וואסער.

אין אנדערע ווערטער, זיי האבן געהאלטן אז יעדע איינציגע נומער, איז אדער א גאנצע נומער אדער א פרעקשן פון אן אנדערע נומער. למשל, די סקווער-רוט פון 2 איז עפעס א פרעקשן פון א נומער וואס מיר דארפן נאך אויסגעפונען, אבער - לדעתם - איז עס זיכער דא.

שפעטער זענען אפיהרגעקומען פארשידענע הוכחות, אז עס זענען פארהאן נומערן וואס זענען זיכער נישט קיין פרעקשן פון קיין שום נומער. (עס איז אביסל טריקי, צו עס אויפווייזן, צוליב דעם וואס איז נישט פשוט מעגליך צו אריבערגיין יעדע מעגליכע נומער, ווייל דאס פיהרט אונז צו אינפיניטי. סא, מ׳מוז צוקומען צו א הוכחה וואס איז בהכרח אויף אלע נומערן אינאיינעם).

לאמיר מצטט זיין די ווערטער פונעם רמב"ם אין פירוש המשניות (עירובין פרק א):

דער רמבם האט געשריבן:יש לך לדעת כי יחוס האלכסון העגולה אל המסבב אותה בלי ידוע, ואי אפשר לדבר בו לעולם באמת, וחסרון זו ההשגה אינה מאתנו כמחשבת הכת הנקראת גהלי"ה, אבל הוא בטבעי זה הדבר בלי ידוע, ואין במציאותו שיושג, אבל ידוע זה בקירוב, וכבר חברו חכמי התשבורת לזה חיבורים לידע יחוס האלכסון אל המופת בקירוב....

כאטש דער רמב"ם איז נישט מוכיח אז עס איז טאקע פארהאן אזא סארט נומער, טענה'ט ער אבער אז עס איז פארהאן, אהן ברענגען א הוכחה דערצו. און ער דערציילט איבער א געוויסע סעקט וואס האבן געהאלטן אז יעדע נומער איז באמת ראציאנאל, נאר מיר ווייסן פשוט נישט די צוויי נומערן (דאס איז די אלטע דיעה וואס מיר האבן פריער דערמאנט).

למעשה – שטעלט זיך ארויס – אז אונזער נומער "די גאלדען רעישיו" קען גענוצט ווערן אז עס איז פארהאן אזא נומער, איבער די הוכחה – און איבער אן אינטרעסאנטע וויכוח צווישן צוויי גדולי תורה - לייענט אינעם קומענדיגן ארטיקל.


[1]. און פאקט, נוצנדיג די שיפע-ליניע פון קאנטאר. ווייסן מיר אז עס זענען פארהאן עפעס אזוי ווי בערך אינסוף מער ריעל-נומערן ווי ראציאנאלע נומערן).
[2]. אין אמת'ן זענען אויך נומערן וואס ווערן נישט געסאלווט פון אן עקוועיזשן, און דאס איז א באזונדערע לענגערע שמועס.

[center]חלק ג[/center]

ווען איך בין דאס ערשטע מאל עקספאזד געווארן צו אט דעם אינטרעסאנטן נומער, איז געווען דורך א תשובה אין חוות יאיר.

דער חוות יאיר און זיינע תשובות אין סימן קע"ב האט א שמועס מיט א מהנדס (אן אינדזשעניר בימים ההם, אין די היינטיגע מושגים בין איך שטארק מסופק אויב ער וואלט אדורכגעגאנגען עלעמענטרי-סקול), איבער דאס וואס דער בעל העיקרים [1] שרייבט אזוי:

כאשר ידבק צלע המעושר עם צלע המשושה, הקו ההוא יחלק על יחס בעל אמצעי ושני קצוות

.

די ווערטער זענען לכאורה זייער סתום, און מאנען א קלארערע הסבר, האט איינער געשריבן דערויף א קונטרס צו מבאר זיין די ווערטער פונעם בעל העיקרים, און דער סך הכל פון יענעמ'ס ווערטער, איז אז אויב גייען מיר נעמען א זייט פון א צעהן-עקיגע פארם + א זייט פון א זעקס-עקיגע פארם, וועלן מיר צוזאמען באקומען א יחס וואס איינס איז אינמיטן, און די צוויי זייטן קענען זיך צוטיילן. (אינעם קומענדיגן פרק וועל איך עס קלארער מאכן).

שרייבט דערויף דער חות יאיר: והוא דבר שוא ושקר וכו' און ער איז דארטן מאריך אז עס איז נישט שייך במציאות עס זאל זיין אזא נומער בכלל, (עיי"ש).

דער בעל מרכבת המשנה האט געשריבן א קונטרס מיטן נאמען ״ברכות בחשבון״, דארטן באציהט ער זיך צו עטליכע מאטעמאטישע עניינים, איינס פון זיי איז טאקע אונזער גאלדען רילעישן, ער ברענגט אראפ די אויבנדערמאנטע תשובה פונעם חוות יאיר. און ער איז זייער שיין מסביר און מוכיח אז עס איז טאקע אזוי.

צום אלעם ערשטן, דארפן מיר מקדים זיין 2 הקדמות:
1). פאר יעדע טריי-ענגל, די סומע פון די מאס פאר זיינע דריי ענגלס איז אייביג 180, נישט מער און נישט ווייניגער.
2). יעדע טריי-ענגל וואס האט צוויי זעלביגע זייטן (משולש שוה שוקיים), דעמאלס זענען די צוויי קעגנזייטיגע ענגלס אויך אייניג. (און אזוי אויך פארקערט יעדע טריי-ענגל וואס האט צוויי זעלביגע ענגלס, דאן זענען די צוויי קעגנזייטיגע זייטן אויך איינ


אינעם קומענדיגן פרק וועל איך איבערגיין די שיינע הוכחה פונעם מרכבת המשנה, האפנטליך עס צו קלאר מאכן, אז יעדער זאל עס קענען פארשטיין נאכן צולייגן אביסל קאפ.



[1]. ער ברענגט דארטן אויך וואס דער רמב"ם שרייבט אין מו"נ ח"א פע"ד, אבער למעשה דאס איז אינגאנצן אן אנדער נושא, און עס איז בכלל נישט נוגע לענייננו.

[center]חלק ד[/center]

לאמיר אויס מאלן א פונקטליכע זעקס-ענגל, דאס איז א פארם וואס באשטייט פון זעקס אייניגע זייטן, (אין בילד: די גרינע פארם), פונעם צענטער ביז יעדע ווינקל איז דא א דיסטענס פון פונקט איין אינטש. אזוי:


עס איז גרינג צו ווערן איבער געצייגט אז יעדע זייט פון די זעקס-ענגל איז אויך 1 אינטש לאנג. וויבאלד אויב מיר צוטיילן די זעקס-ענגל אזוי באקומען מיר זעקס דריי-ענגלס וואס יעדע ענגל איז 60 דיגריס, דאס איז משולש-שווה-צלעות.


יעצט לאמיר ארויינלייגן אין די זעלבע סירקל א צעהן-ענגל, וואס דאס איז א פארם וואס באשטייט פון צעהן אייניגע זייטן, (און די בילד: אויף די רעכטע זייט איז געמאלן א האלבע צעהן-ענגל):



(בדרך אגב, אויב מיר ווילן וויסן וויפיל אינטשעס איז גרויס יעדע איינציגע פון די זייטן, איז גענוג צו איין זעהן אז וויבאלד א סירקל באשטייט פון 360 דיגריס, קענען מיר צוטיילן 360 אין צעהן און באקומען 36, און ווען מיר צוטיילן עס אין 2, באקומען מיר 18. דארפן מיר קאלקולעיטן צוויי מאל סינוס פון 18 דיגריס [1]. (לייג אריין אין א קאלקעלעיטער 18 און דערנאך sin, טיימס 2 [2], און קוק אויב די רעזולטאט איז דיר א באקאנטע נומער)).

לאמיר ציהען ווייטער די ליניע וואס קומט פונעם צענטער און אויך ציהען די אנדער ליניע ווי פאלגענד, גייען מיר באקומען א נייע טרייענגל, לאמיר עס רופן ABC, (לייג צו קאפ צו די בוכשטאבן אין די בילד):



יעצט לאמיר זיך נעמען צו באטראכטן די נייע טריי-ענגל, איז אזוי, ווי מיר האבן מקדים געווען אינעם פריערדיגן פרק, אז דער סומע פון די דריי ענגלס פון יעדע טרייענגל איז אייביג 180.

די טרייענגל, איז 36 דיגריס אין איין ענגל, (ווייל די סירקל איז 360 דיגריס, צוטיילן אין צעהן איז 36), די איבעריגע צוויי ענגלס זענען אייניג, (ווייל די זייטן זענען אויך אייניג), דאן קומט אויס אז יעדע איינס איז 180 מיינוס 36. צוטיילן אין 2, וואס באטרעפט 72.


(איך מוז צוטיילן אין א נייע הודעה צוליב דעם וואס מ'קען נישט אופלאודן מער ווי 5 פיילס).

[1]. איך האב דא היבש סותם געווען, וויבאלד דא איז נישט דאס פלאץ צו אראפשרייבן א ברייטע ערקלערונג ווי אזוי מ׳רעכנט אזעלכע זאכן, ועוד חזון למועד.

[2]. מאך זיכער אז דיין [סייענטיפיק] קאלקעלעיטער איז אנגעשטעלט אויף דיגריס, אויב קענסטו נאר רעכענען אויף ראדיאנס, דאן דארפסטו אויסרעכענען פיי צוטיילן אין צעהן, און דערנאך מאכן sin, און דאן טיימס 2.

ווייסן מיר שוין די מאס פון די ענגלס פאר די אינעווייניגסטע טרייענגל, יעצט לאמיר באטראכטן די ענגלס פאר די דרויסנדע טרייענגל, איז אזוי. וויבאלד יעדע ליין וואס שניידט אדורך אן אנדער גראדע ליין וועט אייביג געבן צוויי ענגלס וואס ביידע צוזאמען באטרעפן 180, אויב אזוי, ווייסן מיר אז די ווינקל f פון די טרייענגל איז 180 מיינוס 72 דיגריס, וואס איז 108 דיגריס.

יעצט כדי צו אויסגעפונען די ווינקל e פון די דרויסנדע טרייענגל, דארפן מיר אנערקענען אז עס איז פארהאן א גראדע ליניע וואס מיר ווייסן שוין אז די צוויי ענגלס באטרעפט יעדע איינס 72, אויב אזוי קומט אויס אז די דריטע ענגל איז 180 מיינוס 2 מאל 72 וואס קומט אויס צו זיין 36.

ווייסן מיר שוין אז איין ענגל איז 36, און איינס איז 72, בלייבט אונז נאר די דריטע וואס איז 180 מיינוס 72 מיינוס 36 וואס קומט אויס צו זיין 36:



יעצט אז מיר ווייסן שוין אז ביידע ענגלס זענען 36, אויב אזוי זענען ביידע זייטן גלייך, אין אנדערע ווערטער - די ליניע איז אזוי גרויס ווי א צלע המעושר.


יעצט זאגט דער בעל ברכות בחשבון, אויב גייען מיר נעמען דעם צלע המשושה, און צולייגן דערצו די צלע המעושר, דאן וועט עס זיין א בעל יחס ושתי קצוות, וואס דאס מיינט אז דו קענסט צוטיילן דעם צלע המשושה אין דעם צלע המשושה פלוס די צלע המעושר, און באקומען די צלע המעושר. וואס דאס איז בעצם אונזער גאלדען רעישיא!!!

און צום סוף וועל איך ברענגען די בילד וואס דער מרכבת המשנה האט געמאלן צו דעם, אפשר וועט עס צוהעלפן פאר מאן דהו:


די זעלבע רעזולטאט קען מען באקומען נאכן זיך ארומשפילן מיט א ״פענטאגראם״, אבער איך קען זיך נישט ערלויבן צו באנוצן מיט אזעלכע טמא׳נע פארמס, ועוד וואס דארפן מיר פראבירן זיין קלוגער פון אונזערע גדולים, וואס האבן אויסגעקליבן דוקא א משושה און א מעושר, ומי יעמוד בסוד קדושים, (ואולי אפשר לומר דהמשושה מרמז על האות ו׳ של שם הוי״ה, וכן המעושר מרמז על אות י׳, והוא רחום יכפר וכו׳).

עס איז כדי אנצומערקן אז אין די באקאנטע פיבאנאטשי סיקווענס [ווי יעדע נומער אין די סיקווענס איז די סומע פון די צוויי נומערן פאר עס] ווי העכער די סיקווענס ווערט, אלס מער ׳עט די רעישיאו פון איין נומער אין די סיקווענס צו איר דערנעבענדיגן נומער אינ׳ם סיקווענס קומען נענטער און נענטער צום גאלדענעם רעישיאו.

*

פארוואס? האט דערמאנט (אין הגה 2 פון חלק ב) די מושג פון טראנסאדענטעל נומערן; נומערן וואס קענען נישט זיין א סאלושען פאר א קוואדראטיק עקוועישאן. עס זענען דא מער טראנסאדענטעל נומערן ווי נישט (באקאנטע זענען pi און e) אבער עס איז זייער שווער אויפצוווייזען אז א ספעסיפיק נומער איז טראנסאדענטעל. וכמובן איז אונזער נומער phi [די גאלדענע רעישיאו] נישט א טראנסאדענטעל נומער, אזוי ווי יידל האט געוואוזען ווען ער האט עס אויפגעוואוזען צו זיין די סאלושען פון א קוואדראטיק עקוועישאן.

נאך א וועג פון מסביר זיין די רעישיאו איז אז מ׳האט צוויי ליינס, איינס גרעסער פון צווייטן, וואס דער גרעסערער צו קלענערער איז א געוויסע רעישיאו (וויפיל ער איז גרעסער פונ׳ם קלענערן). אויב נאכדעם ווען מ׳שטעלט זיי צוזאם ׳עט די מאס פונ׳ם צאמגעשטעלטן ליין זיין די זעלבע רעישיאו צום גרעסערן ליין (לכשלעצמו), דאס איז די גאלדענע רעישיאו.


דאס איז א וויזואלע רעפרעזענטאציע דערפון [די גאלדענע רעישיאו] אין א רעקטענגעל; די גאלדענע רעקטענגעל. די זייט a+b איז [אין לענג - רעישיאו] צו זייט a פונקט אזוי ווי a [אליין] איז צו זייט b. עס איז אינטרעסאנט אז ווען מ׳נעמט אוועק פון די רעקטענגעל א/די חלק פון די גאלדענע רעישיאו (אזוי ווי אין די בילד וואו מ׳נעמט אוועק די a חלק), בלייבט איבער א נייע גאלדענע רעקטענגעל/רעישיאו, וכן הלאה. (די ראיה פונ׳ם מרכבת המשנה, וואס פארוואס? האט אזוי פיין מסביר געווען, טוט קאנסטראקטן א גאלדענע טרייענגעל, ווי די לענגערע זייט[ן - וויבאלד ביידע לענגערע זייטן זענען אייניג לאנג] איז צום קלענערע זייט אין די גאלדענע רעישיאו.)

פארוואס? האט געשריבן:די זעלבע רעזולטאט קען מען באקומען נאכן זיך ארומשפילן מיט א ״פענטאגראם״, אבער איך קען זיך נישט ערלויבן צו באנוצן מיט אזעלכע טמא׳נע פארמס, ועוד וואס דארפן מיר פראבירן זיין קלוגער פון אונזערע גדולים, וואס האבן אויסגעקליבן דוקא א משושה און א מעושר, ומי יעמוד בסוד קדושים, (ואולי אפשר לומר דהמשושה מרמז על האות ו׳ של שם הוי״ה, וכן המעושר מרמז על אות י׳, והוא רחום יכפר וכו׳).

מ׳קען אפשר זאגן, בדרך הלצה, אז די חת״ס זאגט (דרשות לז׳ אב תקע״ב) אז עפ״י קבלה איז א פיס/רגל א צענטל פונ׳ם מענטש און ווי אזוי מ׳מעסט עס איז עס א זעקסטל פונ׳ם מענטש ע״ש. און ווי באקאנט זאגט די גמרא אין שבת לא. אז ווען דער גר האט געפרעגט הלל הזקן שתלמדני כל התורה כולה כשאני עומד על רגל אחת האט ער אים געזאגט דעלך סני לחברך לא תעביד. אין פילאזאפיע ווערט דאס אנגערופן די גאלדענע רול. מ׳קען אפשר מקשר זיין די גאלדענע רעישיאו צו דעם, ווייל עס זענען דא ארטיסטן וואס האלטן אז אעסטעטיש איז די רעישיאו מתקבל על העינים והלב; ענליך צו דעם גאלדענע רול בעניני בין אדם לחבירו.

ואם כנים אנחנו בזה הא׳מיר א שטיקל קשר פארוואס מיט די גאלדענע רעישיאו ניצט מען 10 און 6, ווייל (די inverse) א צענטל און א זעקסטל ווייזן אויף דעם רגל פון א מענטש וכהחת״ס, וואס די גאלדענע רול קען מען לערנען על רגל אחת וכהלל.

מי אני האט געשריבן:פארוואס? האט דערמאנט (אין הגה 2 פון חלק ב) די מושג פון טראנסאדענטעל נומערן; נומערן וואס קענען נישט זיין א סאלושען פאר א קוואדראטיק עקוועישאן. עס זענען דא מער טראנסאדענטעל נומערן ווי נישט (באקאנטע זענען pi און e) אבער עס איז זייער שווער אויפצוווייזען אז א ספעסיפיק נומער איז טראנסאדענטעל. וכמובן איז אונזער נומער phi [די גאלדענע רעישיאו] נישט א טראנסאדענטעל נומער, אזוי ווי יידל האט געוואוזען ווען ער האט עס אויפגעוואוזען צו זיין די סאלושען פון א קוואדראטיק עקוועישאן.

ס׳איז אינטרעסאנט אנצומערקן אז וויבאלד מ׳האט געפּרוּווט אז π איז א טראנסאדענטאל נומער (עפ״י די לינדעמאן-ווייערסטראס טעארעם), איז אלס א פועל יוצא דערפון איז אומעגליך צו סקווערן א סירקל. דאס מיינט עס איז אומעגליך דורך נאר האבן א רוּלער און א קאמפּעס צו האבן א וועג צו נעמען א סקווער און דאס שאפן/מאכן אין צו א סירקעל (מיט די פונקטליך זעלבע עריע), וכן להיפך. ועכ״כ אז עס איז שוין געווארן אן אויסדרוק, ״סקווערן א סירקל״, אויף אויסצודרוקן אז עפעס איז אומעגליך.

‏דאס האט א משהו א שייכות מיט די גמרא אין סוכה ח.

עס לאזט זיך נישט גלייבן די חומר וואס [tag]פארוואס?[/tag] האט דא אראפגלייגט, איך פארשטיי נישט וויאזוי עס איז נישט געווארן מער א שמועס דערפון.

[tag]מי אני[/tag] א דאנק פארן ארויפברענגן און צולייגן משלך. קענסט מסביר זיין מער וועגן transcendental נאמבערס?

צו מסביר זיין (א ביסל בקיצור), דארף מען פריער מסביר זיין די געדאנק פון א פּאלינאמיעל עקוועישאן. דאס איז אן עקספּרעשאן/עקוועישאן וואס מען קען (לאחר הכל) אויסשטעלן אזוי (למשל):
3x⁴+5.34x³-43x²+2x=0
(עס קען פארשטייט זיך האבן x צו אנדערע עקספּאנענטס/דעגריס, און עס קען פעהלן צווישן איין דעגרי אונ׳ם אנדערן. ווי אויך קען עס פארמאגן מער ווי איין וועריעבּל.) יעצט, אין די עקוועישאן, כמובן, באציהט זיך x צו ״עפעס״ א נומער.
לדוגמא, דאס וואס [tag]יידל[/tag] האט געארבעט מיט:
x²-x-1=0
איז א (פשוט׳ע...) פּאלינאמיעל עקוועישאן (אין די פאל קוואדרעטיק, וויבאלד די העכסטע דעגרי/עקספּאָנענט איז 2).

א טראנסעדענטעל נומער איז א נומער וואס איז נישט במציאות צו זיין די x פון קיין שום פּאלינאמיעל עקוועישאן (ווען די קאָעפישענטס [די נומערן וואס מ׳מאָלטיפּלייט די x׳ס ביי] זענען נישט אירעשאנעל). אויפצוווייזן/פּרוּוון אז א נומער איז נישט קיין סאלושאן פאר קיין שום פון די סארט עקוועישאנס איז נישט אזוי פשוט; אביסל ענליך צום אלגעמיינעם שוועריקייט פון אויפווייזן א נעגאטיוו [א ״נישט״] בכלל.

מי אני האט געשריבן:ס׳איז אינטרעסאנט אנצומערקן אז וויבאלד מ׳האט געפּרוּווט אז π איז א טראנסאדענטאל נומער (עפ״י די לינדעמאן-ווייערסטראס טעארעם), איז אלס א פועל יוצא דערפון איז אומעגליך צו סקווערן א סירקל. דאס מיינט עס איז אומעגליך דורך נאר האבן א רוּלער און א קאמפּעס צו האבן א וועג צו נעמען א סקווער און דאס שאפן/מאכן אין צו א סירקעל (מיט די פונקטליך זעלבע עריע), וכן להיפך. ועכ״כ אז עס איז שוין געווארן אן אויסדרוק, ״סקווערן א סירקל״, אויף אויסצודרוקן אז עפעס איז אומעגליך.

‏דאס האט א משהו א שייכות מיט די גמרא אין סוכה ח.

מענין לענין באותו ענין, אז מ׳רעדט פון סירקעלס בתוך סקווערס אין די בילד זענען דא 16 סירקעלס. זיי זענען צווישן די סקווערס. ווי מער די קליינע סקווערס אינדערמיט וואקסן, זענען זייערע עקן די סירקאָמפרענס פונעם סירקעל, דוק ותשכח.

עס איז אינטרעסאנט צו באמערקן אז קארמייקעל׳ס טעארעם לויטעט אז נאך די צוועלעפטע נומער אינעם פיבּאנאטשי סיִקווענס, וואס איז 144, גייט יעדעס פיבּאנאטשי נומער האבן א פּריים דיווייזאר וואס דיווייד נישט קיין איינע פון די פריערדיגע נומערן אינעם סיִקווענס.

***

אויך אביסל ענליך צו די סיִקווענס איז די ווען עק סיִקווענס. דאס ארבעט אזוי: אויב איז די נומער פאר דעם א נייע נומער לייג איך א 0. אויב נישט לייג איך די נומער פון די צאל ווי לאנג צוריק די נומער איז געווען אין די סיִקווענס.

איך הייב אן מיט 0. דערנאך, וויבאלד די נומער פאר דעם [0] איז געווען א נייע נומער, לייג איך א 0. די נעקסטע נומער, די דריטע, קוקט אויף די צווייטע [די 0] און דאס איז נישט א נייע נומער און עס האט שוין פאסירט 1 נומער צוריק, דעריבער לייג איך אן 1. די נעקסטע נומער קוקט אויפ׳ן נומער פריער, דעם 1, וואס איז א נייע נומער אינעם סיִקווענס און דעריבער לייג איך א 0. 0 האט שוין פאסירט 2 נומערן פריער, לייג איך א 2. 2 איז ניי, לייג איך דערנאך א 0, וכן הלאה.

מ׳ווייסט אז די סיִקווענס פארמאגט אינפיניט 0׳ס און אז עס האט נישט חלקים וואס גייען איבער און איבער אין א פּעטערן. מ׳קלערט אז דאס פארמאגט אלע נומערן. ווי אויך קלערט מען אז יעדע צאמשטעל פון צוויי נומערן קומען פאר איינס נאכ׳ן אנדערע, חוץ פון 1 מיט נאך אן 1 נאך דעם, און חוץ פון א נומער מיט די נומער וואס קומט גראד נאך דעם אין די אָרדער [למשל 41 און 42].

אין די געדאנק פון די פיבּאנאטשי סיִקווענס איז דא וואו מ׳קען דאס דזשענערעלייזן צו סיִקווענסעס וואו אנשטאט די נעקסטע עלעמענט אין די סיִקווענס זאל זיין די סומע פון די צוויי פריערדיגע נומערן, זאל עס זיין די סומע פון די דריי פריערדיגע נומערן צו מער (פארשטייט זיך אז דעמאלטס וועל איך אנהייבן סיִדען די סיִקווענס מיט דריי 1׳ס צו מער, ווענדענדיג זיך אין וויפיל פון די פריערדיגע נומערן איך רעכען אנצוקומען צום נעקסטן); אן n-בּאנאטשי סיִקווענס. ביי דריי רוף איך דאס א טריבּאנאטשי סיִקווענס.

אזוי ווי די פיבּאנאטשי סיִקווענס טוהט עפּראקסעמעיטן א ספּיירעל מיט די דימענציעס פון די גאלדענע רעישיאו כנ״ל, האט דער מאטעמאטיקער גערארד ראַוּזי צאמגעשטעלט די טריבּאנאטשי סיִקווענס מיט א סארט פרעקטעל כזה:

וואס ווען איך שטעל צאם דריי דערפון מאכט דאס די אריגינעלע פרעקטעל שׁעיפּ אין גרעסער. דאס ווערט גערופן די ראַוּזי פרעקטעל.

ובענין פּאלינאמיעל עקוועישאנס דא איז א וויץ דערין (בענין אמונה):

*

ווי אויך איז דא אין דעם א סוג וואס רופט זיך דייאָפאנטין עקוועישאנס. דאס זענען פּאלינאמיעל עקוועישאנס וואס די וועריעבּלס זענען נאר אינטעדזשערס [גאנצע פאזיטיווע אדער נעגאטיווע נומערן].

בנוגע פיִבּאָנאטשי נומערן איז דא די זעקענדארף טעארעם. דאס לויטעט אז מען קען ארויסשרייבן יעדעס [נאטורליכע/גאנצע פאזיטיווע] נומער אלס די סומע פון איינס צי מער פיִבּאָנאטשי נומערן. און אויב זענען אלע פיִבּאָנאטשי נומערן וואס מען נוצט אזעלכע וואס זענען נישט נעבן איינע די אנדערע אינעם סיִקווענס איז נאר דא איין וועג ווי אזוי דאס ארויסצושרייבן. למשל, צוצוקומען צו 64 דורך פיִבּאָנאטשי נומערן וואס זענען נישט נעבן איינע די אנדערע אינעם סיִקווענס איז נאר דורכ׳ן נוצן די סומע פון 1, 8, און 55.

דר. לוּאָ מינג האט אויפגעוואוזן אז נאר די נומערן 1,3,21,55 בתוך דעם פיִבּאָנאטשי סיִקווענס זענען טרייענגולאר נומערן.

קיין איין פיִבּאָנאטשי נומער בתוך דעם סיִקווענס איז א פּערפעקט נומער (חוץ די נומער 1). ולא זו בלבד נאר אפילו די רעישיאו און חילוק פון עני צוויי פיִבּאָנאטשי נומערן גייט נישט זיין קיין פּערפעקט נומער.

viewtopic.php?p=463960#p463960